设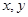 满足约束条件
满足约束条件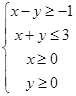 ,求
,求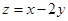 的最大值
的最大值
已知函数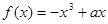 在
在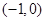 上是增函数.
上是增函数.
⑴求实数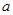 的取值范围
的取值范围 ;
;
⑵当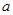 为
为 中最小值时,定义数列
中最小值时,定义数列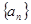 满足:
满足: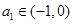 ,且
,且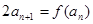 ,
,
用数学归纳法证明 ,并判断
,并判断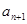 与
与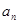 的大小.
的大小.
一个口袋中装有大小形状完全相同的红色球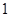 个、黄色球
个、黄色球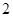 个、蓝色球
个、蓝色球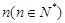 个.现进行从口袋中摸球的游戏:摸到红球得
个.现进行从口袋中摸球的游戏:摸到红球得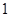 分、摸到黄球得
分、摸到黄球得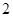 分、摸到蓝球得
分、摸到蓝球得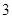 分.若从这个口袋中随机地摸出
分.若从这个口袋中随机地摸出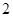 个球,恰有一个是黄色球的概率是
个球,恰有一个是黄色球的概率是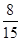 .
.
⑴求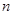 的值;⑵从口袋中随机摸出
的值;⑵从口袋中随机摸出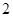 个球,设
个球,设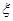 表示所摸
表示所摸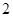 球的得分之和,求
球的得分之和,求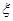 的分布列和数学期望
的分布列和数学期望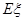 .
.
已知函数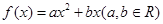 ,函数
,函数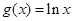 .
.
⑴当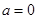 时,函数
时,函数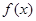 的图象与函数
的图象与函数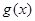 的图象有公共点,求实数
的图象有公共点,求实数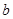 的最大值;
的最大值;
⑵当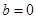 时,试判断函数
时,试判断函数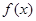 的图象与函数
的图象与函数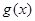 的图象的公共点的个数;
的图象的公共点的个数;
⑶函数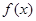 的图象能否恒在函数
的图象能否恒在函数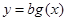 的上方?若能,求出
的上方?若能,求出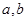 的取值范围;若不能,请说明理由.
的取值范围;若不能,请说明理由.
已知函数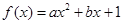 (
(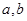 为实数,
为实数,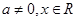 ),
),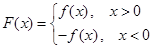 ,⑴若
,⑴若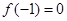 ,且函数
,且函数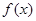 的值域为
的值域为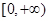 ,求
,求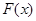 的表达式;
的表达式;
⑵设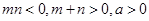 ,且函数
,且函数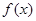 为偶函数,判断
为偶函数,判断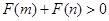 是否大0?
是否大0?
⑶设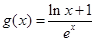 ,当
,当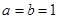 时,证明:对任意实数
时,证明:对任意实数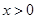 ,
,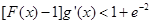 (其中
(其中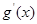 是
是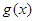 的导函数) .
的导函数) .
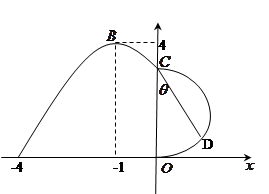
如图,某市新体育公园的中心广场平面图如图所示,在y轴左侧的观光道曲线段是函数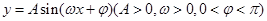 ,
,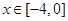 时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,
时的图象且最高点B(-1,4),在y轴右侧的曲线段是以CO为直径的半圆弧.⑴试确定A,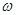 和
和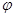 的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设
的值;⑵现要在右侧的半圆中修建一条步行道CDO(单位:米),在点C与半圆弧上的一点D之间设计为直线段(造价为2万元/米),从D到点O之间设计为沿半圆弧的弧形(造价为1万元/米).设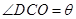 (弧度),试用
(弧度),试用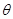 来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)
来表示修建步行道的造价预算,并求造价预算的最大值?(注:只考虑步行道的长度,不考虑步行道的宽度)