已知函数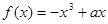 在
在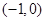 上是增函数.
上是增函数.
⑴求实数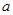 的取值范围
的取值范围 ;
;
⑵当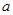 为
为 中最小值时,定义数列
中最小值时,定义数列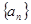 满足:
满足: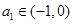 ,且
,且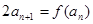 ,
,
用数学归纳法证明 ,并判断
,并判断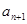 与
与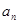 的大小.
的大小.
(本小题满分12分)
某校为宣传县教育局提出的“教育发展,我的责任”教育实践活动,要举行一次以“我
为教育发展做什么”为主题的的演讲比赛,比赛分为初赛、复赛、决赛三个阶段进行,已知
某选手通过初赛、复赛、决赛的概率分别是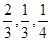 ,且各阶段通过与否相互独立.
,且各阶段通过与否相互独立.
(I)求该选手在复赛阶段被淘汰的概率;
(II)设该选手在比赛中比赛的次数为 ,求
,求 的分布列、数学期望和方差.
的分布列、数学期望和方差.
(本题12分)已知圆C的圆心为C(m,0),(m<3),半径为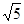 ,圆C与椭圆E:
,圆C与椭圆E: 有一个公共点A(3,1),
有一个公共点A(3,1),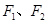 分别是椭圆的左、右焦点;
分别是椭圆的左、右焦点;
(Ⅰ)求圆C的标准方程;
(Ⅱ)若点P的坐标为(4,4),试探究斜率为k的直线 与圆C能否相切,若能,求出椭
与圆C能否相切,若能,求出椭
圆E和直线 的方程,若不能,请说明理由。
的方程,若不能,请说明理由。
本题12分)已知从“神七”飞船带回的某种植物种子每粒成功发芽的概率都为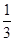 ,某
,某
植物研究所进行该种子的发芽实验,每次实验种一粒种子, 每次实验结果相互独立. 假定某
次实验种子发芽则称该次实验是成功的,如果种子没有发芽,则称该次实验是失败的.若该
研究所共进行四次实验, 设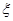 表示四次实验结束时实验成功的次数与失败的次数之差的绝对
表示四次实验结束时实验成功的次数与失败的次数之差的绝对
值.
⑴ 求随机变量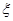 的分布列及
的分布列及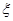 的数学期望
的数学期望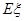 ;
;
⑵ 记“不等式 的解集是实数集
的解集是实数集 ”为事件
”为事件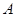 ,求事件
,求事件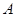 发生的概率
发生的概率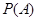 .
.
(本题12分) 已知抛物线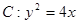 ,顶点为O,动直线
,顶点为O,动直线 与抛物
与抛物
线 交于
交于 、
、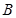 两点
两点
(I)求证: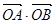 是一个与
是一个与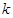 无关的常数;
无关的常数;
(II)求满足 的点
的点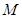 的轨迹方程。
的轨迹方程。
(本题12分)投掷一个质地均匀,每个面上标有一个数字的正方体玩具,它的六个
面中,有两个面的数字是 ,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,
,两个面的数字是2,两个面的数字是4.将此玩具连续抛掷两次,
以两次
朝上一面出现的数字分别作为点P的横坐标和纵坐标.
(1)求点P落在区域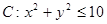 上的概率;
上的概率;
(2)若以落在区域C上的所有点为顶点作面积最大的多边形区域M,在区域C上随机撒一粒
豆子,求豆子落在区域M上的概率.