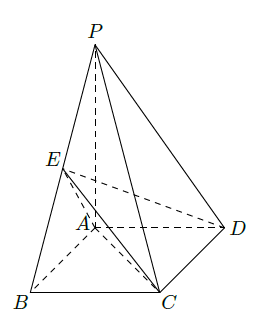
如图，四棱锥PABCD中，底面ABCD为矩形，PA⊥底面AB-优题课

题文

如图，四棱锥 $P - A B C D$ 中，底面 $A B C D$ 为矩形， $P A ⊥$ 底面 $A B C D$ ， $P A = A B = \sqrt{2}$ ，点 $E$ 是棱 $P B$ 的中点.
（Ⅰ）证明： $A E ⊥$ 平面 $P B C$ ；
（Ⅱ）若 $A D = 1$ ，求二面角 $B - E C - D$

科目数学题型解答题难度中等

登录免费查看答案和解析

相关试题

已知点A(3,0)，P是圆上任意一点，∠AOP的平分线交PA于M(O为原点)，试求点M的轨迹.

求一宇宙飞船的轨道，使在轨道上任一点处离地球和月球的视角都相等.

已知圆A的圆心在曲线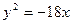上，圆A与y轴相切，又与另一圆相外切，求圆A的方程.

已知与曲线C: x²+y²-2x-2y+1=0相切的直线l与x轴、y轴的正半轴交于两点A、B，O为原点，|OA|＝a，|OB|=b(a>2,b>2)
（1）求证：曲线C与直线l相切的条件是(a-2)(b-2)="2" ;
（2）求ΔAOB面积的最小值。

点A(0,2)是圆x²+y²=16内的定点，点B,C是这个圆上的两个动点，若BA⊥CA,求BC中点M的轨迹方程，并说明它的轨迹是什么曲线。

试卷网试题网古诗词网作文网范文网