已知点A(3,0)，P是圆
上任意一点，∠AOP的平分线交PA于M(O为原点)，试求点M的轨迹.
已知平面向量a=(
,-1),b=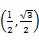
.
(1)若x=(t+2)a+(t2-t-5)b,y=-ka+4b(t,k∈R),且x⊥y,求出k关于t的关系式k=f(t).
(2)求函数k=f(t)在t∈(-2,2)上的最小值.
设a=(cosα,sinα),b=(cosβ,sinβ),若a-b=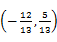
,θ为a与b的夹角.
(1)求θ的值.
(2)若f(x)=2sin(θ-x)cos(θ-x)+2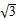
sin2(θ-x),求f(x)的单调递增区间.
已知复平面内平行四边形ABCD(A,B,C,D按逆时针排列),A点对应的复数为2+i,向量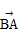
对应的复数为1+2i,向量
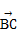对应的复数为3-i.
(1)求点C,D对应的复数.
(2)求平行四边形ABCD的面积.
已知向量
=
,
=
,定义函数f(x)=·.
(1)求函数f(x)的表达式,并指出其最大值和最小值.
(2)在锐角△ABC中,角A,B,C的对边分别为a,b,c,且f(A)=1,bc=8,求△ABC的面积S.
在△ABC中,内角A,B,C的对边分别是a,b,c,且a2=b2+c2+
ab.
(1)求A.
(2)设a=,S为△ABC的面积,求S+3cosBcosC的最大值,并指出此时B的值.