已知点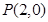 及圆
及圆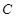 :
: .
.
(Ⅰ)若直线 过点
过点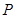 且与圆心
且与圆心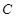 的距离为1,求直线
的距离为1,求直线 的方程;
的方程;
(Ⅱ)设过点P的直线 与圆
与圆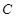 交于
交于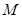 、
、 两点,当
两点,当 时,求以线段
时,求以线段 为直径的圆
为直径的圆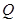 的方程;
的方程;
(Ⅲ)设直线 与圆
与圆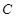 交于
交于 ,
,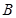 两点,是否存在实数
两点,是否存在实数 ,使得过点
,使得过点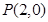 的直线
的直线 垂直平分弦
垂直平分弦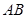 ?若存在,求出实数
?若存在,求出实数 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
(本小题满分12分)为加快新能源汽车产业发展,推进节能减排,某市对消费者购买新能源汽车给予补贴,其中对纯电动乘用车补贴标准如下表:
| 新能源汽车补贴标准 |
|||
| 车辆类型 |
续驶里程 (公里) (公里) |
||
 |
 |
 |
|
| 纯电动乘用车 |
 万元/辆 万元/辆 |
 万元/辆 万元/辆 |
 万元/辆 万元/辆 |
某校研究性学习小组,从汽车市场上随机选取了 辆纯电动乘用车,根据其续驶里程
辆纯电动乘用车,根据其续驶里程 (单次充电后能行驶的最大里程)作出了频率与频数的统计表:
(单次充电后能行驶的最大里程)作出了频率与频数的统计表:
| 分组 |
频数 |
频率 |
 |
 |
 |
 |
 |
 |
 |
 |
 |
| 合计 |
 |
 |
(Ⅰ)求 ,
, ,
, ,
, 的值;
的值;
(Ⅱ)若从这 辆纯电动乘用车中任选
辆纯电动乘用车中任选 辆,求选到的
辆,求选到的 辆车续驶里程都不低于
辆车续驶里程都不低于 公里的概率.
公里的概率.
(本小题满分12分)如图,四棱锥P—ABCD中,PA 平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,M为PC中点,
平面ABCD,底面ABCD是直角梯形,AB⊥AD,CD⊥AD,CD=2AB,M为PC中点,

(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求证:平面PDC 平面PAD.
平面PAD.
(本小题满分14分)经过点 且与直线
且与直线 相切的动圆的圆心轨迹为
相切的动圆的圆心轨迹为 .点
.点 、
、 在轨迹
在轨迹 上,且关于
上,且关于 轴对称,过线段
轴对称,过线段 (两端点除外)上的任意一点作直线
(两端点除外)上的任意一点作直线 ,使直线
,使直线 与轨迹
与轨迹 在点
在点 处的切线平行,设直线
处的切线平行,设直线 与轨迹
与轨迹 交于点
交于点 ,
, .
.
(Ⅰ)求轨迹 的方程;
的方程;
(Ⅱ)证明: ;
;
(Ⅲ)若点 到直线
到直线 的距离等于
的距离等于 ,且△
,且△ 的面积为20,求直线
的面积为20,求直线 的方程.
的方程.
(本小题满分13分)已知函数 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的极值;
的极值;
(Ⅱ)若对任意 ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题满分14分)已知函数 (
( ).
).
(Ⅰ)当 时,求函数
时,求函数 的单调区间;
的单调区间;
(Ⅱ)当 时,
时, 取得极值.
取得极值.
(1)若 ,求函数
,求函数 在
在 上的最小值;
上的最小值;
(2)求证:对任意 ,都有
,都有 .
.