求符合下列条件的抛物线y=ax2-1的函数关系式:
（1）通过点(-3，2)；
（2）与y=
x2的开口大小相同，方向相反；
（3）当x的值由0增加到2时，函数值减少4.
已知：如图，把矩形OCBA放置于直角坐标系中，OC=3，BC=2，取AB的中点M，连结MC，把△MBC沿x轴的负方向平移OC的长度后得到△DAO.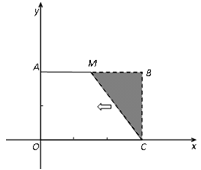
（1）直接写出点D的坐标；
（2）已知点B与点D在经过原点的抛物线上，点P在第一象限内的该抛物线上移动，过点P作PQ⊥x轴于点Q，连结OP.
①若以O、P、Q为顶点的三角形与△DAO相似，试求出点P的坐标；
②试问在抛物线的对称轴上是否存在一点T，使得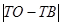
的值最大.若存在，求出T点坐标；若不存在，请说明理由.
已知，如图①，∠MON=60°，点A、B为射线OM、ON上的动点（点A、B不与点O重合），且AB=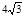
，在∠MON的内部、△AOB的外部有一点P，且AP=BP，∠APB=120°.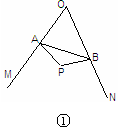
（1）求AP的长；
（2）求证：点P在∠MON的平分线上；
（3）如图②，点C，D，E，F分别是四边形AOBP的边AO，OB，BP，PA的中点，连接CD，DE，EF，FC，OP.
①当AB⊥OP时，请直接写出四边形CDEF的周长；
②若四边形CDEF的周长用t表示，请直接写出t的取值范围．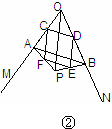
如图，在平面直角坐标系xOy中，抛物线y＝ax2＋bx＋3的顶点为M（2，－1），交x轴于A、B两点，交y轴于点C，其中点B的坐标为（3，0）.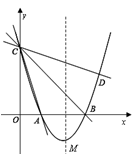
（1）求该抛物线的解析式；
（2）设经过点C的直线与该抛物线的另一个交点为D，且直线CD和直线CA关于直线BC对称，求直线CD的解析式；
（3）在该抛物线的对称轴上存在点P，满足PM2＋PB2＋PC2＝35，求点P的坐标.
操作与实践：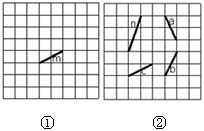
（1）在图①中，以线段m为一边画菱形，要求菱形的顶点均在格点上.（画出所有符合条件的菱形）
（2）在图②中，平移a、b、c中的两条线段，使它们与线段n构成以n为一边的等腰直角三角形.（画一个即可）
，求
的长？