有一座抛物线型拱桥,其水面宽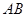 为18米,拱顶
为18米,拱顶 离水面
离水面 的距离
的距离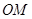 为8米,货船在水面上的部分的横断面是矩形
为8米,货船在水面上的部分的横断面是矩形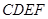 ,如图建立平面直角坐标系.
,如图建立平面直角坐标系.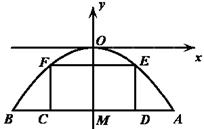
(1)求此抛物线的解析式,并写出自变量的取值范围;
(2)如果限定
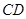 的长为9米,
的长为9米,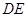 的长不能超过多少米,才能使船通过拱桥?
的长不能超过多少米,才能使船通过拱桥?(3)若设
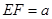 ,请将矩形
,请将矩形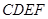 的面积
的面积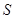 用含
用含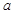 的代数式表示,并指出
的代数式表示,并指出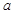 的取值范围.
的取值范围.
已知O为坐标原点,抛物线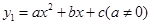 与
与 轴相交于点
轴相交于点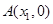 ,
,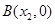 .与
.与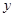 轴交于点C,且O,C两点之间的距离为3,
轴交于点C,且O,C两点之间的距离为3,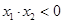 ,
,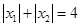 ,点A,C在直线
,点A,C在直线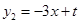 上.
上.
(1)求点C的坐标;
(2)当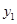 随着
随着 的增大而增大时,求自变量
的增大而增大时,求自变量 的取值范围;
的取值范围;
(3)将抛物线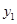 向左平移
向左平移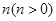 个单位,记平移后
个单位,记平移后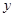 随着
随着 的增大而增大的部分为P,直线
的增大而增大的部分为P,直线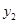 向下平移n个单位,当平移后的直线与P有公共点时,求
向下平移n个单位,当平移后的直线与P有公共点时,求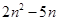 的最小值.
的最小值.
已知反比例函数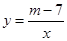 的图象的一支位于第一象限.
的图象的一支位于第一象限.
(1)判断该函数图象的另一支所在的象限,并求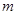 的取值范围;
的取值范围;
(2)如图,O为坐标原点,点A在该反比例函数位于第一象限的图象上,点B与点A关于 轴对称,若
轴对称,若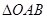 的面积为6,求
的面积为6,求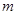 的值.
的值.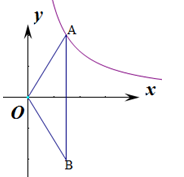
如图,过原点的直线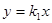 和
和 与反比例函数
与反比例函数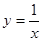 的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
的图象分别交于两点A,C和B,D,连结AB,BC,CD,DA.
(1)四边形ABCD一定是 四边形;(直接填写结果)
(2)四边形ABCD可能是矩形吗?若可能,试求此时 和
和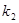 之间的关系式;若不可能,说明理由;
之间的关系式;若不可能,说明理由;
(3)设P(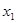 ,
,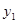 ),Q(
),Q(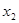 ,
,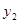 )(
)(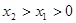 )是函数
)是函数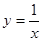 图象上的任意两点,
图象上的任意两点,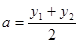 ,
,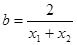 ,试判断
,试判断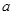 ,
,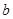 的大小关系,并说明理由.
的大小关系,并说明理由.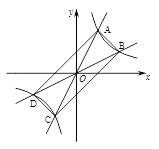

如图,直线 经过点A(4,0),B(0,3).
经过点A(4,0),B(0,3).
(1)求直线 的函数表达式;
的函数表达式;
(2)若圆M的半径为2,圆心M在 轴上,当圆M与直线
轴上,当圆M与直线 相切时,求点M的坐标.
相切时,求点M的坐标.
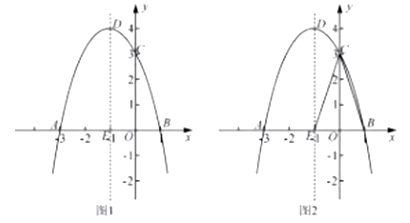
如图1,关于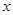 的二次函数y=-
的二次函数y=-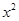 +bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上。
+bx+c经过点A(-3,0),点C(0,3),点D为二次函数的顶点,DE为二次函数的对称轴,E在x轴上。
(1)求抛物线的解析式;
(2)DE上是否存在点P到AD的距离与到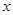 轴的距离相等,若存在求出点P,若不存在请说明理由;
轴的距离相等,若存在求出点P,若不存在请说明理由;
(3)如图2,DE的左侧抛物线上是否存在点F,使2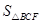 =3
=3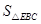 ,若存在求出点F的坐标,若不存在请说明理由。
,若存在求出点F的坐标,若不存在请说明理由。