(10分)(1)如图1,已知点P在正三角形ABC的边BC上,以AP为边作正三角形APQ,连接
CQ.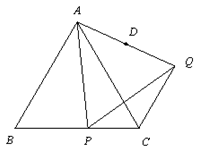
①求证:△ABP≌△ACQ;
②若AB=6,点D是AQ的中点,直接写出当点P由点B运动到点C时,点D运动路线的
长.(2)已知,△EFG中,EF=EG=13,FG=10.如图2,把△EFG绕点E旋转到△EF'G'的位置,点M是边EF'与边FG的交点,点N在边EG'上且EN=EM,连接GN.
求点E到直线GN的距离.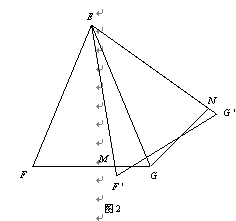
如图,在四边形ABCD中,AC平分∠DAB,CE⊥AB于E.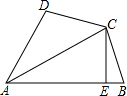
(1)若AB=AD+2BE,求证:BC=DC;
(2)若∠B=60°,AC=7,AD=6,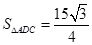 ,求AB的长.
,求AB的长.
A箱中有三张质地相同的卡片,它们分别写有数字-1,-2,3,B箱中装有三张质地相同的卡片,它们分别写有数字1,-1,2.现从A箱,B箱中,各随机地取出一张卡片,请你用画树状图或列表的方法求:
(1)两张卡片上的数字恰好相同的概率;
(2)两张卡片上的数字之积为正数的概率.
如图所示, A 、 B 两地之间有条河,原来从 A 地到 B 地需要经过桥 DC ,沿折线 A → D → C → B 到达.现在新建了桥 EF ,可直接沿直线 AB 从 A 地到达 B 地.已知 BC ="11" km ,∠ A =45°,∠ B =37°,桥 DC 和 AB 平行,则现在从 A 地到 B 地可比原来少走多少路程 (结果精确到0.1 km ,参考数据:  )
) 
已知 ,且
,且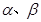 为锐角,求
为锐角,求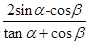 的值 。
的值 。
如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于A、B两点,抛物线y=﹣x2+bx+c经过A、B两点,并与x轴交于另一点C(点C点A的右侧),点P是第二象限的抛物线上一动点.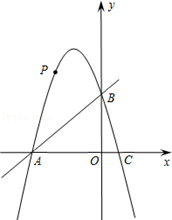
(1)求抛物线的解析式及点C的坐标;
(2)当点P运动到什么位置时,△PAB的面积最大?最大面积是多少?
(3)当(2)中点P运动到△PAB的面积最大时,x轴上是否存在点D,使△PDB的周长最小,若存在,求出点D的坐标,若不存在。请说明理由。