(本题12分)设函数
⑴求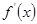 的表达式;
的表达式;
⑵求 的单调区间、极大值、极小值。
的单调区间、极大值、极小值。
(本小题满分12分)为了响应学校“学科文化节”活动,数学组举办了一场数学知识竞赛,共分为甲、乙两组.其中甲组得满分的有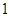 个女生和
个女生和 个男生,乙组得满分的有
个男生,乙组得满分的有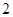 个女生和
个女生和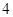 个男生.现从得满分的学生中,每组各任选
个男生.现从得满分的学生中,每组各任选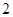 个学生,作为数学组的活动代言人.
个学生,作为数学组的活动代言人.
(1)求选出的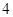 个学生中恰有
个学生中恰有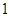 个女生的概率;
个女生的概率;
(2)设 为选出的
为选出的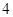 个学生中女生的人数,求
个学生中女生的人数,求 的分布列和数学期望.
的分布列和数学期望.
(本小题满分12分)已知三棱柱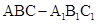 中,侧棱垂直于底面,
中,侧棱垂直于底面,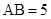 ,
,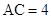 ,
,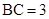 ,
,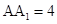 ,点
,点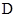 在
在 上.
上.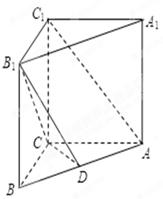
(1)若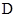 是
是 中点,求证:
中点,求证: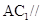 平面
平面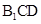 ;
;
(2)当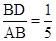 时,求二面角
时,求二面角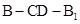 的余弦值.
的余弦值.
(本小题满分12分)已知数列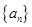 是公差不为
是公差不为 的等差数列,
的等差数列,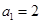 ,且
,且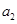 ,
,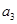 ,
,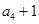 成等比数列.
成等比数列.
(1)求数列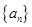 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列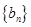 的前
的前 项和
项和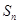 .
.
已知函数f(x)=|x﹣4|﹣t,t∈R,且关于x的不等式f(x+2)≤2的解集为[﹣1,5].
(1)求t值;
(2)a,b,c均为正实数,且a+b+c=t,求证: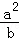 +
+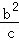 +
+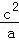 ≥1.
≥1.
在直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知圆C的圆心的极坐标为( ,
,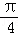 ),半径r=
),半径r= ,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
,点P的极坐标为(2,π),过P作直线l交圆C于A,B两点.
(1)求圆C的直角坐标方程;
(2)求|PA|•|PB|的值.