(本小题满分13分)有一批单放机原价为每台80元,两个商场均有销售,为了吸引顾客,两商场纷纷推出优惠政策。甲商场的优惠办法是:买一台减4元,买两台每台减8元,买三台每台减12元,......,依此类推,直到减到半价为止;乙商场的优惠办法是:一律7折。某单位欲为每位员工买一台单放机,问选择哪个商场购买比较划算?
在平面直角坐标系xOy中,已知曲线C的参数方程为 .以直角坐标系原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为
.以直角坐标系原点为极点,x轴的正半轴为极轴建立极坐标系,直线l的极坐标方程为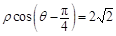 .点P为曲线C上的一个动点,求点P到直线l距离的最小值
.点P为曲线C上的一个动点,求点P到直线l距离的最小值
在 中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
中,AB=AC,过点A的直线与其外接圆交于点P,交BC延长线于点D。
(1)求证:  ;
;
(2)若AC=3,求 的值。
的值。
已知椭圆的离心率 ,左、右焦点分别为
,左、右焦点分别为 ,定点P
,定点P ,点
,点 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线 的倾斜角分别为
的倾斜角分别为 ,求证:直线
,求证:直线 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知函数 .
.
(1)若 ,求函数
,求函数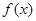 的最大值.
的最大值.
(2)若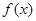 在定义域内为增函数,求实数
在定义域内为增函数,求实数 的取值范围
的取值范围
甲、乙两位学生参加数学竞赛培训.现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次.记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)画出甲、乙两位学生成绩的茎叶图,指出学生乙成绩的中位数;
(2)现要从中选派一人参加数学竞赛,从平均状况和方差的角度考虑,你认为派哪位学生参加合适?请说明理由.