甲、乙两位学生参加数学竞赛培训．现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次．记录如下：
甲：82 81 79 78 95 88 93 84
乙：92 95 80 75 83 80 90 85
（1）画出甲、乙两位学生成绩的茎叶图，指出学生乙成绩的中位数；
（2）现要从中选派一人参加数学竞赛，从平均状况和方差的角度考虑，你认为派哪位学生参加合适?请说明理由．
（1）甲中彩；（2）甲、乙都中彩；（3）乙中彩
（1）请从拥有500个分数的总体中用简单随机抽样方法抽取一个容量为30的样本。
（2）某车间有189名职工，现在要按1：21的比例选派质量检查员，采用系统抽样的方式进行。
（3）一个电视台在因特网上就观众对某一节目喜爱的测得进行得出，车间得出的总人数为12000人，其中持各种态度的人数如下：
很喜爱喜爱一般不喜爱
2435 4567 3926 1072
打算从中抽取60人进行详细调查，如何抽取？
试证：半径等于1 的圆内接三角形中，正三角形的面积最大。
如图，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB∶AD＝
∶1，F是AB的中点．
（1）求VC与平面ABCD所成的角；
（2）求二面角V-FC-B的度数；
（3）当V到平面ABCD的距离是3时，求B到平面VFC的距离．
已知数列{an}满足：
，
．
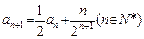⑴求数列{an}的通项公式； ⑵证明：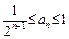
⑶设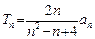
，且
，证明：
．