已知椭圆的离心率 ,左、右焦点分别为
,左、右焦点分别为 ,定点P
,定点P ,点
,点 在线段
在线段 的中垂线上.
的中垂线上.
(1)求椭圆C的方程;
(2)设直线 与椭圆C交于M、N两点,直线
与椭圆C交于M、N两点,直线 的倾斜角分别为
的倾斜角分别为 ,求证:直线
,求证:直线 过定点,并求该定点的坐标.
过定点,并求该定点的坐标.
已知椭圆
 的离心率为
的离心率为 ,一个焦点为
,一个焦点为 .
.
(Ⅰ)求椭圆 的方程;
的方程;
(Ⅱ)设直线 交椭圆
交椭圆 于
于 ,
, 两点,若点
两点,若点 ,
, 都在以点
都在以点 为圆心的圆上,求
为圆心的圆上,求 的值.
的值.
如图,矩形 中,
中, ,
, .
. ,
, 分别在线段
分别在线段 和
和 上,
上, ∥
∥ ,将矩形
,将矩形 沿
沿 折起.记折起后的矩形为
折起.记折起后的矩形为 ,且平面
,且平面 平面
平面 .
.
(Ⅰ)求证: ∥平面
∥平面 ;
;
(Ⅱ)若 ,求证:
,求证: ;
;
(Ⅲ)求四面体 体积的最大值.
体积的最大值.

某校高一年级开设研究性学习课程,(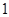 )班和(
)班和(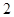 )班报名参加的人数分别是
)班报名参加的人数分别是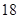 和
和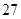 .现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(
.现用分层抽样的方法,从中抽取若干名学生组成研究性学习小组,已知从(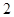 )班抽取了
)班抽取了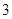 名同学.
名同学.
(Ⅰ)求研究性学习小组的人数;
(Ⅱ)规划在研究性学习的中、后期各安排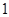 次交流活动,每次随机抽取小组中
次交流活动,每次随机抽取小组中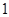 名同学发言.求
名同学发言.求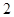 次发言的学生恰好来自不同班级的概率.
次发言的学生恰好来自不同班级的概率.
在△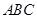 中,已知
中,已知 .
.
(Ⅰ)求角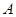 ;
;
(Ⅱ)若 ,△
,△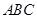 的面积是
的面积是 ,求
,求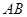 .
.
对于数列 ,定义“
,定义“ 变换”:
变换”: 将数列
将数列 变换成数列
变换成数列 ,其中
,其中 ,且
,且 ,这种“
,这种“ 变换”记作
变换”记作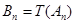 .继续对数列
.继续对数列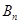 进行“
进行“ 变换”,得到数列
变换”,得到数列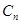 ,…,依此类推,当得到的数列各项均为
,…,依此类推,当得到的数列各项均为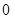 时变换结束.
时变换结束.
(Ⅰ)试问 和
和 经过不断的“
经过不断的“ 变换”能否结束?若能,请依次写出经过“
变换”能否结束?若能,请依次写出经过“ 变换”得到的各数列;若不能,说明理由;
变换”得到的各数列;若不能,说明理由;
(Ⅱ)求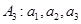 经过有限次“
经过有限次“ 变换”后能够结束的充要条件;
变换”后能够结束的充要条件;
(Ⅲ)证明: 一定能经过有限次“
一定能经过有限次“ 变换”后结束.
变换”后结束.