已知函数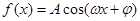 (
(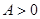 ,
,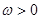 ,
,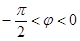 )的图像与
)的图像与 轴的交点
轴的交点
为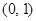 ,它在
,它在 轴右侧的第一个最高点和第一个最低点的坐标分别为
轴右侧的第一个最高点和第一个最低点的坐标分别为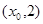 和
和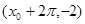
(1)求函数 的解析式;
的解析式;
(2)若锐角 满足
满足 ,求
,求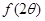 的值.
的值.
已知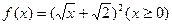 ,数列
,数列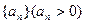 的前
的前 项和
项和
(1)求数列 的通项公式;
的通项公式;
(2)若 ,
, ,求
,求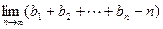 的值.
的值.
已知椭圆 的中心在坐标原点
的中心在坐标原点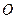 ,一条准线的方程为
,一条准线的方程为 ,过椭圆的左焦点
,过椭圆的左焦点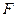 ,且方向向量为
,且方向向量为 的直线
的直线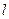 交椭圆于
交椭圆于 两点,
两点,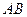 的中点为
的中点为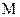
(1)求直线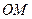 的斜率(用
的斜率(用 、
、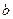 表示);
表示);
(2)设直线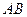 与
与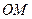 的夹角为
的夹角为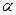 ,当
,当 时,求椭圆的方程.
时,求椭圆的方程.
在“灿烂阳光小歌手PK赛”10进6的比赛中,有男歌手和女歌手各3人进入前6名,现从中任选2名歌手去参加2010年的元旦联欢会的演出,求:
(1)恰有一名参赛歌手是男歌手的概率;
(2)至少有一名参赛歌手是男歌手的概率;
(3)至多有一名参赛歌手是男歌手的概率.
2008年在中国北京成功举行了第29界奥运赛,其中乒乓球比赛实行五局三胜的规则,即先胜三局的获胜,比赛到此宣布结束。在赛前,有两个国家进行了友谊赛,比赛双方并没有全部投入主力,两队双方较强的队伍每局取胜的概率为0.6,若前四局出现2比2平局,较强队就更换主力,则其在决赛局中获胜的概率为0.7,设比赛结束时的局数为
(1)求 的概率分布;
的概率分布;
(2)求E .
.
造船厂年造船量20艘,造船 艘产值函数为
艘产值函数为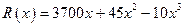 (单位:万元),成本函数
(单位:万元),成本函数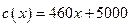 (单位:万元),又在经济学中,函数
(单位:万元),又在经济学中,函数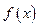 的边际函数
的边际函数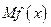 定义为
定义为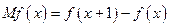
(1)求利润函数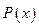 及边际利润函数
及边际利润函数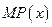 (利润=产值—成本)
(利润=产值—成本)
(2)问年造船量安排多少艘时,公司造船利润最大
(3)边际利润函数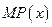
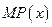 的单调递减区间
的单调递减区间