(8分)在东西方向的海岸线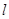 上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距
上有一长为1km的码头MN(如图),在码头西端M 的正西19.5 km 处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于 A 的北偏西30°,且与A相距40km的B处;经过1小时20分钟,又测得该轮船位于A的北偏东60°,且与A相距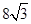 km的C处.
km的C处.
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
如图,晚间小明站在距离路灯5m(即BD=5m)的地面上,发现他的影子长DF为4m.已知小明的身高为1.6m,如果小明再向远离路灯的方向走4m,则此时小明的影长是多少?
王亮同学利用课余时间对学校旗杆的高度进行测量,他是这样测量的:把长为3m的标杆垂直放置于旗杆一侧的地面上,测得标杆底端距旗杆底端的距离为15m,然后往后退,直到视线通过标杆顶端刚好看到旗杆顶端时为止,测得此时人与标杆的水平距离为2m,已知王亮的身高为1.6m,请帮他计算旗杆的高度.(王亮眼睛距地面的高度视为他的身高)
一位同学想利用树的影长测量树高,他在某一时刻测得长为1m的竹竿的影长为0.9m,但当他马上测量树的影长时,因树靠近一幢建筑物,影子不全落在地面上,有一部分影子落在墙上,如图,他先测得留在墙上的影子高CD为1.2m,又测得地面上的影子长BC为2.7m,则树高AB为多少?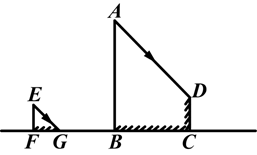
如图,在△ABC中,点D是AB的中点,点E在边AC上,且∠AED=∠ABC,如果AE=3,EC=1,求边AB的长.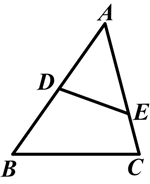
如图所示,在△ABC中,AB=4,探究以下问题:
(1)如图①所示,DE∥BC,DE把△ABC分成面积相等的两部分,即S1=S2,求AD的长;
(2)如图②所示,DE∥FG∥BC,DE,FG把△ABC分成面积相等的三部分,即S1=S2=S3,求AD的长;
(3)如图③所示,DE∥FG∥HK∥…∥BC,DE,FG,HK,…把△ABC分成面积相等的n部分,即S1=S2=S3=…=Sn,请直接写出AD的长.