某商场为吸引顾客消费推出一项优惠活动.活动规则如下：消费额每满100元可转动如图所示的圆盘一次，并获得相应金额的返券，假定指针等可能地停在任一位置. 若指针停在A区域返券60元；停在B区域返券30元；停在C区域不返券. 例如：消费218元，可转动圆盘2次，所获得的返券金额是两次金额之和.
（1）若某位顾客消费128元，求返券金额不低于30元的概率；
（2）若某位顾客恰好消费280元，并按规则参与了活动，他获得返券的金额记
为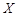
（元）.求随机变量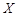的分布列和数学期望.
（本小题12分）
甲、乙两位学生参加数学竞赛培训，在活动期间，他们参加的5次测试成绩记录如下：
甲 82 82 79 95 87乙 95 75 80 90 85
⑴用茎叶图表示这两组数据；
⑵若要从中选派一人参加数学竞赛，从统计学的角度考虑，你认为选派哪位学生参加合适？说明理由。
（本小题12分）一个盒子中装有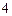
张卡片，每张卡片上写有
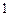个数字，数字分别是、
、
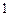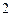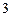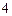、。现从盒子中随机抽取卡片，
⑴若一次抽取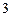张卡片，求张卡片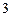上数字之和大于
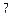的概率；
⑵若第一次抽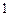张卡片，放回后再抽取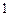张卡片，求两次抽取中至少一次抽到数字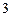的概率。
（本小题12分）已知命题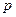
：函数
的图象与
轴没有公共点，命题
，若命题
为真命题，求实数
的取值范围
（本小题满分14分）
已知函数
R
, 
.
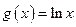（1）求函数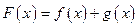
的单调区间；
（2）若关于
的方程
为自然对数的底数)只有一个实数根, 求
的值.
（本小题满分14分）如图直线l：y＝x＋b与抛物线C：x2＝4y相切于点A.
(1)求实数b的值；
(2)求以点A为圆心，且与抛物线C的准线相切的圆的方程．