如图,在△BCD中,∠BCD=90°,BC=CD=1,AB⊥平面BCD,∠ADB=60°,E、F分别是AC、AD上的动点,且==λ(0<λ<1).
(1)判断EF与平面ABC的位置关系并给予证明;
(2)是否存在λ,使得平面BEF⊥平面ACD,如果存在,求出λ的值,如果不存在,说明理由.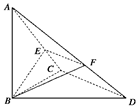
已知直线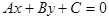 ,
,
(1)系数为什么值时,方程表示通过原点的直线;
(2)系数满足什么关系时与坐标轴都相交;
(3)系数满足什么条件时只与x轴相交;
(4)系数满足什么条件时是x轴;
(5)设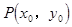 为直线
为直线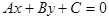 上一点,
上一点,
证明:这条直线的方程可以写成 .
.
已知一条曲线在x轴的上方,它上面的每一点到点A(0,2)的距离减去它到x轴的距离的差都是2,求这条曲线的方程.
用坐标法证明三角形的中位线长为其对应边长的一半.
判断下列A(-1,-1),B(0,1),C(1,3)三点是否共线,并给出证明.
已知点P (x, y),则求①关于y轴的对称点;②关于x轴的对称点;③关于原点的对称点;④关于直线y = x的对称点;⑤关于直线y=-x的对称点(-y, -x).