(本题10分)
如图,梯形ABCD中,AD∥BC,BC=2AD,F、G分别为边BC、CD的中点,连接AF,FG,过D作DE∥GF交AF于点E。
(1)证明△AED≌△CGF
(2)若梯形ABCD为直角梯形,判断四边形DEFG是什么特殊四边形?并证明你的结论。
ΔABC中,∠B=300,∠C=450,并且AB-AC=4-2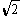 .求ΔABC的面积.
.求ΔABC的面积. 
某公司推出了一种高效环保型洗涤用品,年初上市后,公司经历了从亏损到盈利的过程,下面的二次函数的图象(部分)刻画了该公司年初以来累积利润S(万元)与销售时间t(月)之间的关系(即前t个月的利润总和S与t之间的关系).
(1)根据图象你可获得哪些关于该公司的具体信息?(至少写出三条)
(2)还能提出其他相关的问题吗?若不能,说明理由;若能,进行解答,并与同伴交流.
如图,一位篮球运动员跳起投篮,球沿抛物线y=-x2+3.5运行,然后准确落入框内。已知篮框的中心离地面的距离为3.05米。求: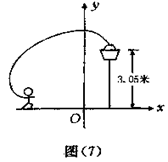
(1)球在空中运行的最大高度为多少米?
(2)如果该运动员跳投时,球出手离地面的高度为2.25米,请问他距离篮框中心的水平距离是多少?
已知二次函数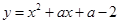 ,求证:它的图象与x轴总有两个交点。
,求证:它的图象与x轴总有两个交点。
抛物线y=ax2+bx+c与直线y=x-2相交于(m,-2),(n,3)两点,且抛物线的对称轴为直线x=3,求抛物线的解析式。