 如图,已知关于
如图,已知关于 的一元二次函数
的一元二次函数 (
(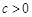 )的图象与
)的图象与 轴相交于
轴相交于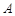 、
、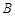 两点(点
两点(点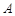 在点
在点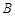 的左侧),与
的左侧),与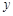 轴交于点
轴交于点 ,且
,且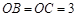 ,顶点为
,顶点为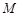 .
.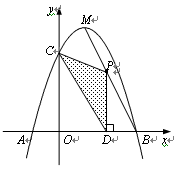
⑴ 求出一元二次函数的关系式;
⑵
 点
点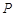 为线段
为线段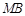 上的一个动点,过点
上的一个动点,过点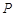 作
作 轴的垂线
轴的垂线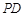 ,垂足为
,垂足为 .若
.若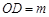 ,
,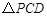 的面积为
的面积为 ,求
,求 关于
关于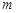 的函数关系式,并写出
的函数关系式,并写出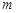 的取值范围;
的取值范围;⑶ 探索线段
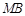 上是否存在点
上是否存在点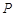 ,使得
,使得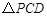 为直角三角形,如果存在,求出
为直角三角形,如果存在,求出 的坐标;如果不存在,请说明理由.
的坐标;如果不存在,请说明理由.
解方程组 .
.
把下列各式进行因式分解:
(1)3ax2-6axy+3ay2;
(2)x2(x-y)+(y-x).
计算:(3x2)2•(-4y3)÷(6xy)2.
在平面直角坐标系中,点A在y轴正半轴上,点B与点C都在x轴上,且点B在点C的左侧,满足BC=OA,若-3am-1b2与anb2n-2是同类项且OA=m,OB=n.
(1)m=;n=.
(2)点C的坐标是.
(3)若坐标平面内存在一点D,满足△BCD全等△ABO,试求点D的坐标.
如图,在△ABC中,∠ACB=90°,CD⊥AB于D.把三角形沿AE对折使点C落在AB边上的点F上,CD与折痕AE相交于G,连结FG并延长交AC于H.
(1)判断FH与BC的位置关系,并说明理由;
(2)判断HG与DG的数量关系,并说明理由.