如图所示,电源的电动势E=10V,内电阻r=1Ω,电容器的电容C=40μF,定值电阻R1=R2=4Ω,R3=5Ω。当接通开关S,待电路稳定后,试求: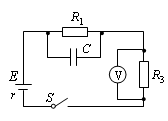
理想电压表V的示数
 ;
;电容器所带的电荷量。
如图所示,静止放在水平桌面上的纸带,其上有一质量为m="0.1" kg的铁块,它与纸带右端的距离为L=0.5m,所有接触面之间的动摩擦因数相同。现用水平向左的恒力,经2s时间将纸带从铁块下抽出,当纸带全部抽出时铁块恰好到达桌面边缘且速度为v=2m/s。已知桌面高度为H=0.8m,不计纸带重力,铁块视为质点。重力加速度g取10m/s2,求: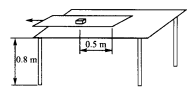
(1)铁块抛出后落地点离抛出点的水平距离;
(2)动摩擦因数;
(3)纸带抽出过程中系统产生的内能。
如图甲所示,间距为 L、电阻不计的光滑导轨固定在倾角为 q的斜面上。在 MNPQ矩形区域内有方向垂直于斜面的匀强磁场,磁感应强度为 B;在 CDEF矩形区域内有方向垂直于斜面向下的磁场,磁感应强度 Bt 随时间 t变化的规律如图乙所示,其中 Bt的最大值为 2B。现将一根质量为 M、电阻为 R、长为 L的金属细棒 cd跨放在 MNPQ区域间的两导轨上并把它按住,使其静止。在 t=0 时刻,让另一根长也为 L的金属细棒 ab从 CD上方的导轨上由静止开始下滑,同时释放 cd棒。已知 CF长度为 2L,两根细棒均与导轨良好接触,在 ab从图中位置运动到 EF处的过程中,cd棒始终静止不动,重力加速度为 g;tx是未知量。
(1)求通过 cd棒的电流,并确定 MN PQ区域内磁场的方向;
(2)当 ab棒进入 CDEF区域后,求 cd棒消耗的电功率;
(3)求 ab棒刚下滑时离 CD的距离。
四川某中学物理兴趣小组同学开展研究性学习,对常在火车站看到载重列车启动时,机车首先要倒退的问题进行调查,最后得出结论:因为机车和车厢与铁轨之间的最大静摩擦力大于它们之间的动摩擦力,若机车不倒退直接启动,启动以后机车和车厢与铁轨之间的摩擦力由静摩擦力变为动摩擦力,当列车加速到一定的速度后,列车的机车就必须减少牵引力使列车匀速直线运动,资源不能得到充分的利用,所以载重列车常常采用先倒退的启动方式启动。现假设有一列载重列车,若它不倒退以恒定的牵引力直接启动,机车的牵引力能带动49节车厢(不含机车),那么它利用倒退后用同样大小的恒定牵引力启动,该机车启动59节同样质量的车厢以后,恰好做匀速直线运动,已知机车与各节车厢的质量均为m,机车和各节车厢与铁轨之间的动摩擦力为 ,假设机车倒退后,各节车厢之间的挂钩离开相同的距离
,假设机车倒退后,各节车厢之间的挂钩离开相同的距离 ,机车加速后,每拉动一节车厢的瞬间可近似地认为满足动量守恒定律的条件。求:
,机车加速后,每拉动一节车厢的瞬间可近似地认为满足动量守恒定律的条件。求:
(1)每一节车厢与铁轨之间的最大静摩擦力?
(2)列车采用机车倒退的方式启动后做匀速直线运动的速度?(最终结果可以用根式表示)
2011年9月29日,我国在酒泉卫星发射中心成功发射了“天宫1号”目标飞行器, 11月3日凌晨,“天宫一号”目标飞行器与“神舟八号”飞船第一对接成功,标志着中国航天朝着建立国际空间站迈出了意义非凡的一步。国际空间站是迄今世界上最大的航天工程,它是地球大气层上空环绕地球飞行的一个巨大的人造天体,可供宇航员在其上居住和进行科学实验。已知地球质量为 ,半径为
,半径为 ,自转角速度为
,自转角速度为 ,万有引力恒量为
,万有引力恒量为 ,如果规定物体在离地球无穷远处势能为零,则质量为
,如果规定物体在离地球无穷远处势能为零,则质量为 的物体离地心距离为
的物体离地心距离为 时,具有的引力势能
时,具有的引力势能 。设空间站离地面高度为
。设空间站离地面高度为 ,如果在该空间站直接发射一颗质量为
,如果在该空间站直接发射一颗质量为 的小卫星,使其能达到地球同步卫星轨道并能在轨道上正常运行,则该卫星正在离开空间站时必须具有多大的动能?
的小卫星,使其能达到地球同步卫星轨道并能在轨道上正常运行,则该卫星正在离开空间站时必须具有多大的动能?
如图所示,光滑水平面上有两辆车,甲车上面有发射装置,甲车连同发射装置质量M1=1kg,车上另有一个质量为m=0.2kg的小球。甲车静止在平面上,乙车以V0=8m/s的速度向甲车运动,乙车上有接收装置,总质量M2=2kg,问:甲车至少以多大的水平速度将小球发射到乙车上,两车才不会相撞?(球最终停在乙车上) 