已知双曲线C：
，
(1) 求双曲线C的渐近线方程；
(2) 已知点M的坐标为(0,1)．设P是双曲线C上的点，Q是点P关于原点的对称点．记
,求λ的取值范围；
(3) 已知点D、E、M的坐标分别为(－2，－1)、(2，－1)、(0,1)，P为双曲线C上在第一象限内的点．记l为经过原点与点P的直线，s为△DEM截直线l所得线段的长．试将s表示为直线l的斜率k的函数．
是否存在等差数列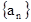
，使
对任意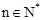
都成立？若存在，求出数列
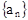的通项公式；若不存在，请说明理由．
已知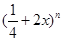
的展开式中前三项的二项式系数的和等于37，求展式中二项式系数最大的项的系数．
若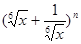
展开式中第二、三、四项的二项式系数成等差数列．
求n的值；
（２）此展开式中是否有常数项，为什么？
三个女生和五个男生排成一排．
（1）如果女生必须全排在一起，有多少种不同的排法？
（2）如果女生必须全分开，有多少种不同的排法？
（3）如果两端都不能排女生，有多少种不同的排法？
（4）如果两端不能都排女生，有多少种不同的排法？
（5）如果三个女生站在前排，五个男生站在后排，有多少种不同的排法？
一场晚会有5个唱歌节目和3个舞蹈节目，要求排出一个节目单
（1）前4个节目中要有舞蹈，有多少种排法？
（2） 3个舞蹈节目要排在一起，有多少种排法？
（3） 3个舞蹈节目彼此要隔开，有多少种排法？