已知直线l过点P（3，4）
(1)它在y轴上的截距是在x轴上截距的2倍，求直线l的方程.
(2)若直线l与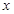
轴，
轴的正半轴分别交于点
，求
的面积的最小值.
已知函数
（1）若k=2，求方程
的解；
（2）若关于x方程
上有两个解
，求k取值范围并证明
椭圆
的左、右焦点分别为F1、F2，离心率
右准线为
M、N是
上的两个点，
（1）若
，求椭圆方程；
（2）证明，当|MN|取最小值时，向量
与
共线.
棱长为1的正方体ABCD—A1B1C1D1中，P为DD1的中点，O1、O2、O3分别为平面A1B1C1D1、平面BB1C1C、平面ABCD的中心.
（1）求PO2的长。
（2）求证：B1O3⊥PA；
（3）求异面直线PO3与O1O2所成的角；
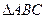的三边a、b、c和面积S满足关系式：
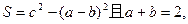求面积S的最大值.
本题满分12分）
等差数列
的各项均为正数，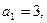
，前n项和为
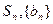是等比数列，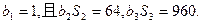
（1）求列数和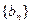
的通项公式；
（2）求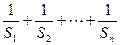
的值.