椭圆 的左、右焦点分别为F1、F2,离心率
的左、右焦点分别为F1、F2,离心率 右准线为
右准线为 M、N是
M、N是 上的两个点,
上的两个点,
(1)若 ,求椭圆方程;
,求椭圆方程;
(2)证明,当|MN|取最小值时,向量 与
与 共线.
共线.
已知等差数列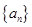 满足:
满足: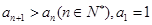 ,该数列的前三项分别加上l,l,3后顺次成为等比数列
,该数列的前三项分别加上l,l,3后顺次成为等比数列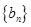 的前三项.
的前三项.
(I)求数列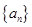 ,
,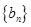 的通项公式;
的通项公式;
(II)设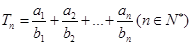 ,若
,若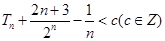 恒成立,求c的最小值.
恒成立,求c的最小值.
在四棱锥P-ABCD中,侧面PCD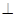 底面ABCD,PD
底面ABCD,PD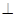 CD,底面ABCD是直角梯形,AB∥DC,
CD,底面ABCD是直角梯形,AB∥DC,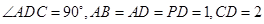 ADC-900,AB=AD=PD=1.CD=2.
ADC-900,AB=AD=PD=1.CD=2.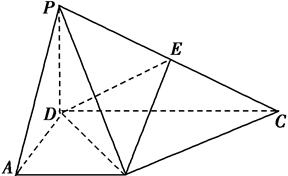
(I)求证:BC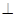 平面PBD:
平面PBD:
(II)设E为侧棱PC上异于端点的一点,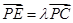 ,试确定
,试确定 的值,使得二面角
的值,使得二面角
E-BD-P的大小为 .
.
已知函数 .
.
(I)若函数 为奇函数,求实数
为奇函数,求实数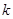 的值;
的值;
(II)若对任意的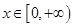 ,都有
,都有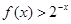 成立,求实数
成立,求实数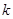 的取值范围.
的取值范围.
在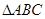 中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.
中,角A、B、C的对边分别为a、b、c,且角A、B、C成等差教列.
(I)若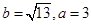 ,求边c的值;
,求边c的值;
(II)设 ,求
,求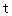 的最大值.
的最大值.
已知函数 在
在 上是增函数,
上是增函数,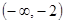 上是减函数.
上是减函数.
(1)求函数 的解析式;
的解析式;
(2)若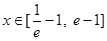 时,
时, 恒成立,求实数m的取值范围;
恒成立,求实数m的取值范围;
(3)是否存在实数b,使得方程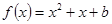 在区间
在区间 上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.
上恰有两个相异实数根,若存在,求出b的范围,若不存在说明理由.