甲盒中有一个红色球,两个白色球,这3个球除颜色外完全相同,有放回地连续抽取2个,每次从中任意地取出1个球,用列表的方法列出所有可能结果,计算下列事件的概率。
(1)取出的2个球都是白球; (2)取出的2个球中至少有1个白球.
在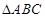 中,角
中,角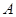 、
、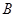 、
、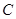 所对的边分别为
所对的边分别为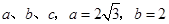 ,
,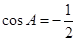 .
.
(1)求角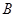 的大小;
的大小;
(2)若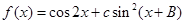 ,求函数
,求函数 的最小正周期和单调递增区间.
的最小正周期和单调递增区间.
已知椭圆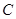 方程为
方程为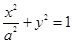 ,过右焦点斜率为1的直线到原点的距离为
,过右焦点斜率为1的直线到原点的距离为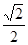 .
.
(1)求椭圆方程.
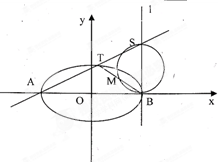
(2)已知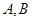 为椭圆的左右两个顶点,
为椭圆的左右两个顶点,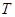 为椭圆在第一象限内的一点,
为椭圆在第一象限内的一点,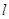 为过点
为过点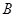 且垂直
且垂直 轴的直线,点
轴的直线,点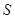 为直线
为直线 与直线
与直线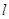 的交点,点
的交点,点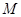 为以
为以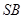 为直径的圆与直线
为直径的圆与直线 的一个交点,求证:
的一个交点,求证: 三点共线.
三点共线.
已知
(1)若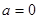 时,求函数
时,求函数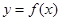 在点
在点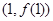 处的切线方程;
处的切线方程;
(2)若函数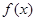 在
在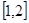 上是减函数,求实数
上是减函数,求实数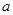 的取值范围;
的取值范围;
(3)令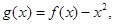 是否存在实数
是否存在实数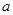 ,当
,当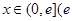 是自然对数的底)时,函数
是自然对数的底)时,函数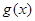 的最小值是3,
的最小值是3,
若存在,求出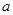 的值;若不存在,说明理由.
的值;若不存在,说明理由.
设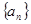 是正数组成的数列,
是正数组成的数列, .若点
.若点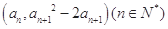 在函数
在函数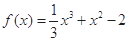 的导函数
的导函数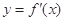 图像上.
图像上.
(1)求数列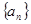 的通项公式;
的通项公式;
(2)设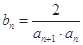 ,是否存在最小的正数
,是否存在最小的正数 ,使得对任意
,使得对任意
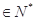 都有
都有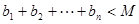 成立?请说明理由.
成立?请说明理由.
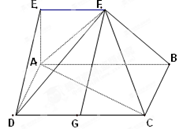
如图,在多面体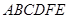 中,四边形
中,四边形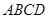 是矩形,
是矩形,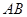 ∥
∥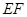 ,
,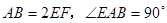 ,平面
,平面 .
.
(1)若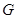 点是
点是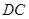 中点,求证:
中点,求证: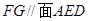 .
.
(2)求证: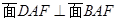 .
.
(3)若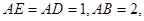 求
求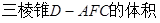 .
.