(本小题满分12分)
如图,在底面为直角梯形的四棱锥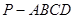 中,
中,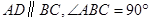 ,
,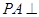 平面
平面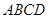 ,
, ,
,
(1) 求证: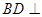 平面
平面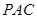 ;
;
(2) 求二面角 的大小.
的大小. 
如图,已知抛物线C: ,
,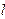 为其准线,过其对称轴上一点P
为其准线,过其对称轴上一点P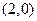 作直线
作直线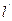 与抛物线交于A
与抛物线交于A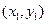 、B
、B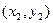 两点,连结OA、OB并延长AO、BO分别交
两点,连结OA、OB并延长AO、BO分别交 于点M、N。(1)求
于点M、N。(1)求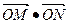 的值;
的值;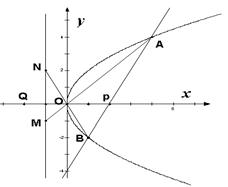
(2)记点Q是点P关于原点的对称点,
设P分有向线段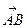 所成的比为
所成的比为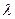 ,
,
且 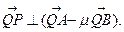 求证:
求证: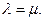
设数列{an},{bn}都是等差数列,它们的前n项的和分别为Sn , Tn,若对一切n ∈ N*,都有Sn+3 = Tn.(1)若a1 ≠ b1,试分别写出一个符号条件的数列{an}和{bn};(2)若a1 + b1 = 1,数列{cn}满足:cn = 4 an + l(–1)n–12bn,且当n ∈ N*时,cn+1 ≥ cn恒成立,求实数l的最大值.
设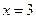 是函数
是函数 的一个极值点。
的一个极值点。
(1)求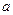 与
与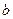 的关系式(用
的关系式(用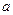 表示
表示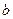 ),并求
),并求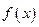 的单调区间;(2)设
的单调区间;(2)设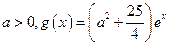 ,若存在
,若存在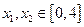 ,使得
,使得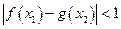 成立,求
成立,求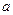 的取值范围。
的取值范围。
已知,三棱锥P-ABC中,侧棱PC与底面成600的角,AB⊥AC,BP⊥AC,AB=4,AC=3. 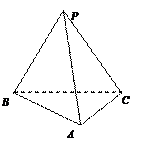
(1) 求证:截面ABP⊥底面ABC;(2)求三棱锥P-ABC的体积的最小值,及此时二面角A-PC-B的正切值.
 中,角
中,角 所对的边分别为
所对的边分别为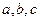 且
且 (1)求角的
(1)求角的 大小(2)若向量
大小(2)若向量 ,向量
,向量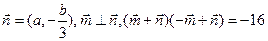 ,求
,求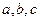 的值
的值