(本小题满分12分)
已知数列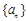 的前n项和为
的前n项和为 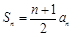 (n∈N*),且
(n∈N*),且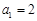 .数列
.数列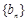 满足
满足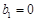 ,
,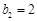 ,
,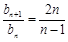 ,n=2,3,….
,n=2,3,….
(Ⅰ)求数列 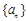 的通项公式;
的通项公式;
(Ⅱ)求数列 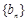 的通项公式;
的通项公式;
(Ⅲ)证明:对于  ,
,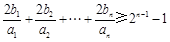 .
.
(本小题12分)
在锐角△ABC中,a、b、c分别为角A、B、C所对的边,且
(1)求角C的大小;
(2)若c=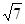 ,且△ABC的面积为
,且△ABC的面积为
 ,求a+b的值。
,求a+b的值。
(理科题)(本小题12分)
已知数列{an}是等差数列,a2=3,a5=6,数列{bn}的前n项和是Tn,且Tn+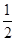 bn=1.
bn=1.
(1)求数列{an}的通项公式与前n项的和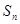 ;
;
(2)求数列{bn}的通项公式.
(文科题)(本小题12分)
(1)在等比数列{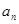 }中,
}中,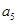 =162,公比q=3,前n项和
=162,公比q=3,前n项和 =242,求首项
=242,求首项 和项数n的值.
和项数n的值.
(2)已知 是数列
是数列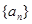 的前n项和,
的前n项和, ,求
,求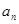
(本小题12分)
已知 ,
, .
.
(1)求 ;
;
(2)若不等式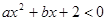 的解集是
的解集是 ,求实数
,求实数 ,
,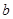 的值
的值
已知数列 满足,
满足,
证明: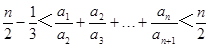 ,(
,(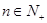 )
)