（本小题满分12分）已知数列{an}的前n项和为Sn，且an是Sn与2的等差中项，数列{bn}中，b1=1，点P（bn，bn+1）在直线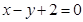
上。
（1）求a1和a2的值；
（2）求数列{an}，{bn}的通项an和bn；
（3）设cn=an·bn，求数列{cn}的前n项和Tn.
已知复数
，
，求复数
实部的最值.
求方程ax2＋2x＋1＝0有且只有一个负实数根的充要条件
指出下列各组命题中，p是q的什么条件？
(1)p：(x－2)(x－3)＝0；q：x－2＝0.
(2)p：四边形的对角线相等；q：四边形是平行四边形．
(3)p：m<－2，q：方程x2－x－m＝0无实根．
分别写出下列命题的逆命题、否命题、逆否命题，并判断它们的真假．
(1)若x、y都是奇数，则x＋y是偶数；
(2)若x>2，y>3，则x＋y>5.
若集合A＝{x|x2－2x－8＜0}，B＝{x|x－m＜0}．
(1)若m＝3，全集U＝A∪B，试求A∩(∁UB)；
(2)若A∩B＝∅，求实数m的取值范围；
(3)若A∩B＝A，求实数m的取值范围．