(本题8分)已知正方形ABCD中，E为对角线BD上一点，过E-优题课

(本题8分)已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．

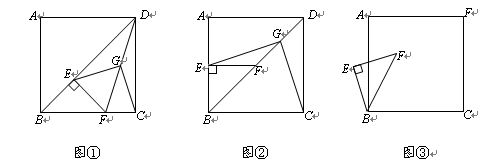
（1）求证：EG=CG；
（2）将图①中△BEF绕B点逆时针旋转45º，如图②所示，取DF中点G，连接EG，CG．
（3）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由．
（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论？（本小问均不要求证明）

科目数学题型解答题难度中等

知识点：圆内接四边形的性质

如图，抛物线 $y = a x^{2} + bx + c$ 与 $x$ 轴交于点 $A (- 1, 0)$ ，点 $B (- 3, 0)$ ，且 $OB = OC$ ．

（1）求抛物线的解析式；

（2）点 $P$ 在抛物线上，且 $∠ POB = ∠ ACB$ ，求点 $P$ 的坐标；

（3）抛物线上两点 $M$ ， $N$ ，点 $M$ 的横坐标为 $m$ ，点 $N$ 的横坐标为 $m + 4$ ．点 $D$ 是抛物线上 $M$ ， $N$ 之间的动点，过点 $D$ 作 $y$ 轴的平行线交 $MN$ 于点 $E$ ．

①求 $DE$ 的最大值；

②点 $D$ 关于点 $E$ 的对称点为 $F$ ，当 $m$ 为何值时，四边形 $MDNF$ 为矩形．

如图，在正方形 $ABCD$ 中，点 $E$ 是 $AB$ 边上一点，以 $DE$ 为边作正方形 $DEFG$ ， $DF$ 与 $BC$ 交于点 $M$ ，延长 $EM$ 交 $GF$ 于点 $H$ ， $EF$ 与 $CB$ 交于点 $N$ ，连接 $CG$ ．

（1）求证： $CD ⊥ CG$ ；

（2）若 $\tan ∠ MEN = \frac{1}{3}$ ，求 $\frac{MN}{EM}$ 的值；

（3）已知正方形 $ABCD$ 的边长为1，点 $E$ 在运动过程中， $EM$ 的长能否为 $\frac{1}{2}$ ？请说明理由．

在“我为祖国点赞“征文活动中，学校计划对获得一，二等奖的学生分别奖励一支钢笔，一本笔记本．已知购买2支钢笔和3个笔记本共38元，购买4支钢笔和5个笔记本共70元．

（1）钢笔、笔记本的单价分别为多少元？

（2）经与商家协商，购买钢笔超过30支时，每增加1支，单价降低0.1元；超过50支，均按购买50支的单价售，笔记本一律按原价销售．学校计划奖励一、二等奖学生共计100人，其中一等奖的人数不少于30人，且不超过60人，这次奖励一等奖学生多少人时，购买奖品总金额最少，最少为多少元？

如图，在 $ΔABC$ 中，以 $AC$ 为直径的 $⊙ O$ 交 $AB$ 于点 $D$ ，连接 $CD$ ， $∠ BCD = ∠ A$ ．

（1）求证： $BC$ 是 $⊙ O$ 的切线；

（2）若 $BC = 5$ ， $BD = 3$ ，求点 $O$ 到 $CD$ 的距离．

双曲线 $y = \frac{k}{x} (k$ 为常数，且 $k \neq 0)$ 与直线 $y = - 2 x + b$ ，交于 $A (- \frac{1}{2} m$ ， $m - 2)$ ， $B (1, n)$ 两点．

（1）求 $k$ 与 $b$ 的值；

（2）如图，直线 $AB$ 交 $x$ 轴于点 $C$ ，交 $y$ 轴于点 $D$ ，若点 $E$ 为 $CD$ 的中点，求 $ΔBOE$ 的面积．