(本题8分)一个实验室在0:00—2:00保持20℃的恒温,在2:00—4:00匀速升温,每小时升高5℃,写出时间t(单位:时)与实验室温度T(单位:℃)之间的函数解析式,并画出图象。
我们知道多项式的乘法可以利用图形的面积进行解释,如(2a+b)(a+b)=2a2+3ab+b2就能用图1或图2等图形的面积表示: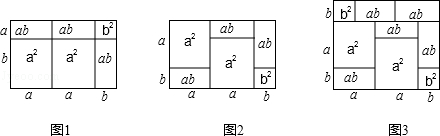
(1)请你写出图3所表示的一个等式: .
(2)试画出一个图形,使它的面积能表示:(a+b)(a+3b)=a2+4ab+3b2.
心理学家研究发现,在一节45分钟的课中,学生的注意力随教师讲课的时间的变化而变化,开始学生的注意力逐渐增强,中间学生的注意力保持稳定的状态,随后开始分散,经实验学生的注意力指数y随时间x(分钟)的变化规律如图所示.
(1)一位教师为了达到最好的上课效果,准备课前复习,要求学生的注意力指数至少达到30时,开始上新课,问他应该复习多长时间?
(2)如果(1)的这位教师本节新课内容需要22分钟,为了使学生的听课效果最好,问这位教师能否在学生听课效果最好时,讲完新课内容?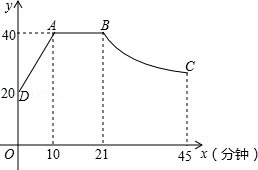
如图,已知一次函数y1=x+m(m为常数)的图象与反比例函数 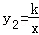 (k为常数,k≠0)的图象相交于点 A(1,3).
(k为常数,k≠0)的图象相交于点 A(1,3).
(1)求这两个函数的解析式及其图象的另一交点B的坐标;
(2)点C(a,b)在反比例函数 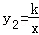 的图象上,求当1≤a≤3时,b的取值范围;
的图象上,求当1≤a≤3时,b的取值范围;
(3)观察图象,写出使函数值y1≥y2的自变量x的取值范围.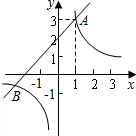
已知y=y1﹣y2,且y1与x的算术平方根成正比例,y2与x的平方成反比例,当x=1时,y=0;x=2时,y=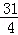 ,求y关于x的表达式.
,求y关于x的表达式.
已知变量y与2x成反比例,且当x=2时,y=6,
(1)求y与x之间的函数关系.
(2)请判断点B(3,4)是否在这个反比例函数的图象上,并说明理由.