．八年级数学活动小组为了调查居民的用水情况，从某社区的1500户家庭中随机抽取了30户家庭的月用水量，结果如
下表所示：
| 月用水量（吨） |
3 |
4 |
5 |
7 |
8 |
9 |
10 |
| 户数 |
4 |
3 |
5 |
11 |
4 |
2 |
1 |
（1）求这30户家庭月用水量的平均数、众数和中位数；
（2）根据上述数据，试估计该社区的月用水量；
（3）由于我国水资源缺乏，许多城市常利用分段计费的办法引导人们节约用水，即规定每个家庭的月基本用水量为m（吨），家庭月用水量不超过m（吨）的部分按原价收费，超过m（吨）的部分加倍收费。你认为上述问题中的平均数、众数和中位数中哪一个量作为月基本用水量比较合理？简述理由。
四边形ABCD是平行四边形，E是对角线AC上一点，射线DE分别交射线CB、AB于点F、G．
（1）如图，如果点F在CB边上，点G在AB边的延长线上，求证：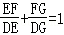
；
（2）如果点F在CB边的延长线上，点G在AB边上，试写出
与
之间的一种等量关系，并给出证明．
如图，AB是半圆O的直径，点M是半径OA的中点，点P在线段AM上运动（不与点M重合），点Q在半圆O上运动，且总保持PQ=PO，过点Q作⊙O的切线交BA的延长线于点C．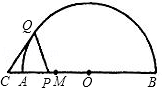
（1）当∠QPA=60°时，请你对△QCP的形状做出猜想，并给予证明；
（2）当QP⊥AB时，△QCP的形状是 三角形；
（3）由（1）、（2）得出的结论，请进一步猜想当点P在线段AM上运动到任何位置时，△QCP一定是 三角形．
如图在直角坐标系中，矩形OABC的顶点O与坐标原点重合，顶点A，C在坐标轴上，顶点B的坐标为（4，2）．过点D（0，3）和E（6，0）的直线分别与AB，BC交于点M，N．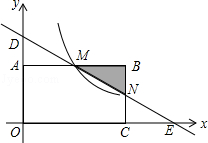
（1）求点M的坐标；
（2）若反比例函数 y=
（x＞0）的图象经过点M，通过计算判断点N是否在该函数的图象上；
（3）在（2）的条件下观察图形，当x取何值时，一次函数值小于反比例函数值．
如图（1），格点△ABC（顶点在小正方形的顶点处的三角形称为格点三角形），请在图（2）、（3）、（4）中的6×6的网格中各画一个互不全等的格点三角形，使它们都和△ABC相似．
要求：①其中有一个相似比为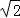
；②其中有一个面积为5．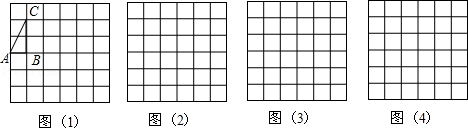
已知O是平面直角坐标系的原点，点A（1，n），B（﹣1，﹣n）（n＞0），AB的长是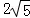
，若点C在x轴上，且OC=AC，求点C的坐标．