如图,已知抛物线 经过O(0,0),A(4,0),B(3,
经过O(0,0),A(4,0),B(3, )三点,连接AB,过点B作BC∥
)三点,连接AB,过点B作BC∥ 轴交该抛物线于点C.
轴交该抛物线于点C.

求这条抛物线的函数关系式.
两个动点P、Q分别从O、A同时出发,以每秒1个单位长度的速度运动. 其中,点P沿着线段0A向A点运动,点Q沿着线段AB向B点运动. 设这两个动点运动的时间为
 (秒) (0<
(秒) (0< ≤2),△PQA的面积记为S.
≤2),△PQA的面积记为S.
① 求S与 的函数关系式;
的函数关系式;
② 当 为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
为何值时,S有最大值,最大值是多少?并指出此时△PQA的形状;
是否存在这样的
 值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
值,使得△PQA是直角三角形?若存在,请直接写出此时P、Q两点的坐标;若不存在,请说明理由.
如图,点B、C、D都在⊙O上,过点C作AC∥BD交OB延长线于点A,连接CD,且∠CDB=∠OBD=30°,DB=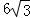 cm.
cm.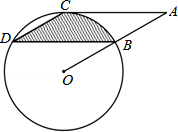
(1)求证:AC是⊙O的切线;
(2)求由弦CD、BD与弧BC所围成的阴影部分的面积.(结果保留π)
图1、图2是两张形状、大小完全相同的方格纸,方格纸中的每个小正方形的边长均为1,点A和点B在小正方形的顶点上.请你在图1、图2中各画出一个直角三角形,使所画两直角三角形的形状不同(另一顶点为小正方形的顶点).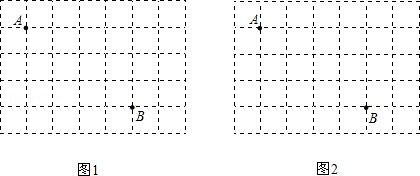
(1)计算:(﹣2)﹣1﹣|﹣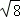 |+(
|+( ﹣1)0+cos45°.
﹣1)0+cos45°.
(2)已知m2﹣5m﹣14=0,求(m﹣1)(2m﹣1)﹣(m+1)2+1的值.
如图,在平面直角坐标系xoy中,抛物线y=ax2+bx﹣4与x轴交于点A(﹣2,0)和点B,与y轴交于点C,直线x=1是该抛物线的对称轴.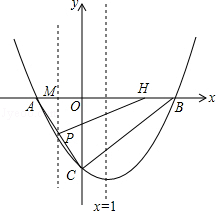
(1)求抛物线的解析式;
(2)若两动点M、H分别从点A、B以每秒1个单位长度的速度沿x轴同时出发相向而行,当点M到达原点时,点H立刻掉头,并以每秒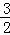 个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
个单位长度的速度向点B方向移动,当点M到达抛物线的对称轴时,两点停止运动,经过点M的直线l⊥x轴,交AC或BC于点P,设点M的运动时间为t秒(t>0).求点M的运动时间t与△APH的面积S的函数关系式,并求出S的最大值.
在等腰直角三角形ABC中,∠BAC=90°,AB=AC,直线MN过点A且MN∥BC,过点B为一锐角顶点作Rt△BDE,∠BDE=90°,且点D在直线MN上(不与点A重合),如图1,DE与AC交于点P,易证:BD=DP.(无需写证明过程)
(1)在图2中,DE与CA延长线交于点P,BD=DP是否成立?如果成立,请给予证明;如果不成立,请说明理由;
(2)在图3中,DE与AC延长线交于点P,BD与DP是否相等?请直接写出你的结论,无需证明.