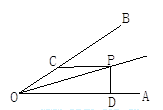如图,抛物线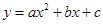 与
与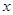 轴交于
轴交于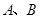 两点,与
两点,与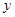 轴相交于点
轴相交于点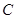 .连结AC、BC,B、C两点的坐标分别为B(1,0)、
.连结AC、BC,B、C两点的坐标分别为B(1,0)、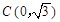 ,且当x=-10和x=8时函数的值
,且当x=-10和x=8时函数的值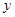 相等.
相等.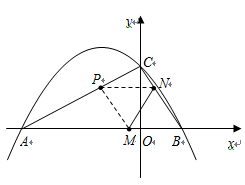
求a、b、c的值;
若点
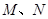 同时从
同时从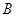 点出发,均以每秒1个单位长度的速度分别沿
点出发,均以每秒1个单位长度的速度分别沿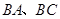 边运动,其中一个点到达终点时,另一点也随之停止运动.连结
边运动,其中一个点到达终点时,另一点也随之停止运动.连结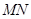 ,将
,将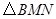 沿
沿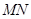 翻折,当运动时间为几秒时,
翻折,当运动时间为几秒时,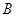 点恰好落在
点恰好落在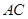 边上的
边上的 处?并求点
处?并求点 的坐标及四边形
的坐标及四边形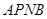 的面积;
的面积;上下平移该抛物线得到新的抛物线,设新抛物线的顶点为D,对称轴与x轴的交点为E,若△ODE与△OBC相似,求新抛物线的解析式。
计算与解方程(每小题4分,共24分)
(1)
(2)
(3)-9÷3+( -
- )+32
)+32
(4)6x=3x-12
(5)
(6)
(本题10分)如图,已知梯形ABCD中,AD∥BC,∠A=90°,AD=2,AB=BC=4,在线段AB上有一动点E,设BE ,△DEC的面积为
,△DEC的面积为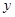 ,问:
,问: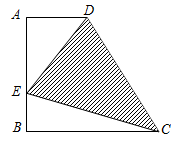
(1)你能找出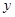 与
与 的函数关系吗?(写出自变量
的函数关系吗?(写出自变量 的取值范围)
的取值范围)
(2)△DEC的面积可能等于5吗?说明你的理由.
(3)探究何时△DEC的面积取得最大(小)值,并求出相应的最大(小)值
如图,△ABC中,D是BC的中点,过D点的直线GF交AC于F,交AC的平行线
BG于G点,DE⊥DF,交AB于点E,连结EG、EF.
(1)求证:BG=CF.
(2)请你判断BE+CF与EF的大小关系,并说明理由.
如图,直线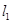 与
与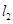 相交于点P,
相交于点P,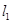 的函数表达式y=2x+3,点P的横坐标为-1,且
的函数表达式y=2x+3,点P的横坐标为-1,且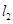 交y轴于点A(0,1).求直线
交y轴于点A(0,1).求直线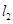 的函数表达式.
的函数表达式.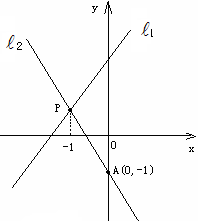
如图所示,∠AOP=∠BOP=15°,PC∥OA,PD⊥OA,若PC=4,求PD的长.