(本小题14分)已知四棱锥P-ABCD,底面ABCD是 、边长为
、边长为 的菱形,又
的菱形,又 ,且PD=CD,点M、N分别是棱AD、PC的中点.
,且PD=CD,点M、N分别是棱AD、PC的中点.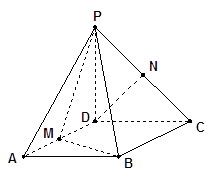
(1)证明:DN//平面PMB;
(2)证明:平面PMB 平面PAD;
平面PAD;
(3)求点A到平面PMB的距离.
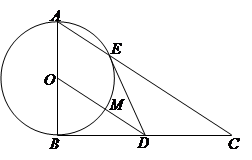
如图,在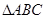 中,
中,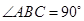 ,以
,以 为直径的圆
为直径的圆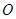 交
交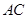 于点
于点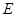 ,点
,点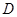 是
是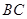 边的中点,连接
边的中点,连接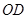 交圆
交圆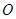 于点
于点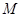 .
.
(Ⅰ)求证: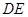 是圆
是圆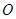 的切线;
的切线;
(Ⅱ)求证: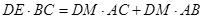 .
.
(本小题满分12分)设函数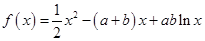 (其中
(其中 为自然对数的底数,
为自然对数的底数,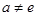 ,
,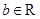 ),曲线
),曲线 在点
在点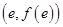 处的切线方程为
处的切线方程为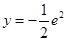 .
.
(1)求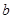 的值;
的值;
(2)若对任意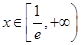 ,函数
,函数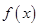 有且只有两个零点,求
有且只有两个零点,求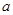 的取值范围.
的取值范围.
(本小题满分12分)已知椭圆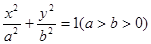 的左、右焦点分别是
的左、右焦点分别是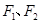 ,其离心率
,其离心率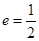 ,点
,点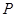 为椭圆上的一个动点,
为椭圆上的一个动点,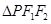 面积的最大值为
面积的最大值为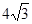 .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若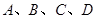 是椭圆上不重合的四个点,
是椭圆上不重合的四个点,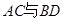 相交于点
相交于点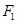 ,
,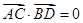 ,求
,求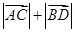 的取值范围.
的取值范围.
(本小题满分12分)已知数列{ }的前n项和为
}的前n项和为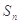 ,且满足
,且满足 .
.
(Ⅰ)证明:数列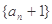 为等比数列,并求数列{
为等比数列,并求数列{ }的通项公式;
}的通项公式;
(Ⅱ)数列{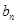 }满足
}满足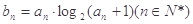 ,其前n项和为
,其前n项和为 ,试求满足
,试求满足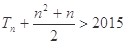 的最小正整数n.
的最小正整数n.
(本小题满分12分) 如图,已知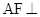 平面
平面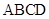 ,四边形
,四边形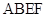 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形,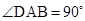 ,
,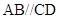 ,
,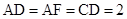 ,
,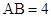 .
.
(Ⅰ)求证: 平面
平面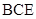 ;
;
(Ⅱ)求三棱锥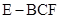 的体积.
的体积.