(本小题满分12分)
已知向量
(I)若 求
求
(II)求 的最大值。
的最大值。
已知锐角△ABC中,角 A.B.C所对边分别是a.b.c,
A.B.C所对边分别是a.b.c,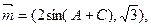
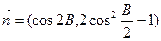 ,且
,且 ∥
∥
(1)求角B的大小;
(2)如果b=1,求△ABC面积的最大值。
数列 的前n项和记为
的前n项和记为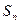 ,
,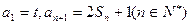
(1)t为何值时,数列 是等比数列?
是等比数列?
(2)在(1)的条件下,若等差数列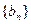 的前n项和
的前n项和 有最大值,且
有最大值,且 ,又
,又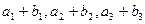 成等比数列,求
成等比数列,求 。
。
(本小题满分14分)
已知函数
(1)求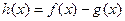 的单调区间;
的单调区间;
(2)求证:当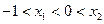 时,
时,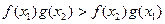 ;
;
(3)求证:
(本小题满分12分)
已知函数
(1)若 求
求 的单调区间及
的单调区间及 的最小值;
的最小值;
(2)求 的单调区间;
的单调区间;
(3)试比较 的大小,
的大小, ,并证明你的结论。
,并证明你的结论。
(本小题满分12)
设二次函数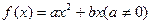 满足条件:
满足条件:
①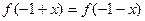 ;②函数
;②函数 的图象与直线
的图象与直线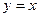 只有一个公共点。
只有一个公共点。
(1)求 的解析式;
的解析式;
(2)若不等式 时恒成立,求实数
时恒成立,求实数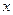 的取值范围。
的取值范围。