在平面直角坐标系中△ABC的边AB在x轴上，且OA>OB,以AB为直径的圆过点C，若C的坐标为(0,2),AB="5," A,B两点的横坐标XA,XB是关于X的方程
的两根:
求m，n的值;
若∠ACB的平分线所在的直线
交x轴于点D，试求直线对应的一次函数的解析式;过点D任作一直线
分别交射线CA，CB（点C除外）于点M，N，则
的值是否为定值，若是，求出定值，若不是，请说明理由
如图，在Rt△ABC中，∠ACB＝90°，点D，F分别在AB，AC上，CF＝CB．连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．
（1）求证：△BCD≌△FCE；
（2）若EF∥CD．求∠BDC的度数．
小美周末来到公园,发现在公园一角有一种“守株待兔”游戏．游戏设计者提供了一只兔子和一个有A、B、C、D、E五个出入口的兔笼，而且笼内的兔子从每个出入口走出兔笼的机会是均等的．规定①玩家只能将小兔从A、B两个出入口放入，②如果小兔进入笼子后选择从开始进入的出入口离开，则可获得一只价值5元小兔玩具，否则应付费3元．
（1）问小美得到小兔玩具的机会有多大?
（2）假设有100人次玩此游戏, 估计游戏设计者可赚多少元?
某校抽样调查了部分初三学生的升学意向，调查结果有三种情况：A．考上三星级高中；B．考取四星级高中；C．进入职业技术学校．教务处将调查数据进行了整理，绘制了如下不完整的统计图．请根据相关信息，
解答下列问题：
（1）本次活动共调查了学生名；
（2）求出图②中B区域圆心角的度数；
（3）若该校初三学生共有600名，请用样本估计该校学生中目标“考取四星级高中”的人数．
（1）解方程：（1）x2－6x＋8="0" ；（2）解不等式组：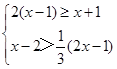
；
（1）
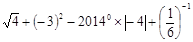； （2）（x+2）2+x（2﹣x）；