已知两条直线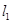 :
: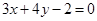 与
与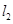 :
: 的交点
的交点 ,求满足下列条件的直线方程
,求满足下列条件的直线方程
(1)过点P且过原点的直线方程;
(2)过点P且垂直于直线 :
: 直线
直线 的方程;(10分)
的方程;(10分)
提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度 (单位:千米/小时)是车流密度
(单位:千米/小时)是车流密度 (单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当
(单位:辆/千米)的函数.当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0千米/小时;当车流密度不超过20辆/千米时,车流速度为60千米/小时.研究表明:当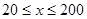 时,车流速度
时,车流速度 是车流密度
是车流密度 的一次函数.
的一次函数.
(Ⅰ)当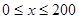 时,求函数
时,求函数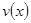 的表达式;
的表达式;
(Ⅱ)当车流密度 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)
为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)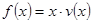 可以达到最大,并求出最大值.(精确到1辆/小时).
可以达到最大,并求出最大值.(精确到1辆/小时).
甲,乙,丙三位学生独立地解同一道题,甲做对的概率为 ,乙,丙做对的概率分别为
,乙,丙做对的概率分别为 ,
,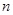 (
( >
>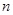 ),且三位学生是否做对相互独立.记
),且三位学生是否做对相互独立.记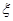 为这三位学生中做对该题的人数,其分布列为:
为这三位学生中做对该题的人数,其分布列为:
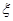 |
0 |
1 |
2 |
3 |
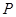 |
 |
 |
 |
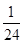 |
(Ⅰ)求至少有一位学生做对该题的概率;
(Ⅱ)求 ,
,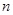 的值;
的值;
(Ⅲ)求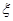 的数学期望.
的数学期望.
已知向量 =(
=(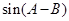 ,
, ),
), =(1,
=(1, ),且
),且

 =
=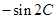 ,其中
,其中 、
、 、
、 分别为
分别为 的三边
的三边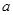 、
、 、
、 所对的角.
所对的角.
(Ⅰ)求角 的大小;
的大小;
(Ⅱ)若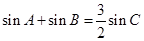 ,且
,且 ,求边
,求边 的长.
的长.
已知 ,函数
,函数
(1)求曲线 在点
在点 处的切线方程; (2)当
处的切线方程; (2)当 时,求
时,求 的最大值.
的最大值.
知椭圆 的左右焦点为F1,F2,离心率为
的左右焦点为F1,F2,离心率为 ,以线段F1 F2为直径的圆的面积为
,以线段F1 F2为直径的圆的面积为 , (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.
, (1)求椭圆的方程;(2) 设直线l过椭圆的右焦点F2(l不垂直坐标轴),且与椭圆交于A、B两点,线段AB的垂直平分线交x轴于点M(m,0),试求m的取值范围.