(12分)如图7-15,在正三棱柱ABC—A1B1C1中,各棱长都等于a,D、E分别是AC1、BB1的中点,
(1)求证:DE是异面直线AC1与BB1的公垂线段,并求其长度;
(2)求二面角E—AC1—C的大小;
(3)求点C1到平面AEC的距离。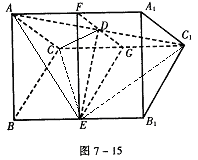
数列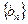 前n项和为
前n项和为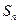 且
且
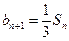
(1)求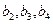 的值;
的值;
(2)求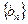 的通项公式;
的通项公式;
(3)求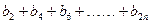 值;
值;
A、B、C为△ABC的三个内角,且其对边分别为a、b、c,
若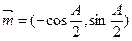
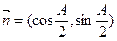 且
且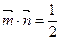
(1)求角A的大小;
(2)若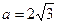 ,三角形面积
,三角形面积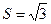 ,求
,求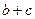 的值。
的值。
已知集合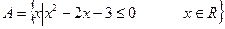
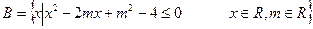
(1)若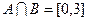 求实数m的值;
求实数m的值;
(2)若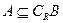 求实数m取值范围。
求实数m取值范围。
已知数列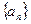 中,
中, 且点
且点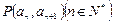 在直线
在直线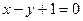 上.
上.
(1)求数列 的通项公式;
的通项公式;
(2)若函数
求函数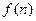 的最小值;
的最小值;
(3)设 表示数列
表示数列 的前
的前 项和.试问:是否存在关于
项和.试问:是否存在关于 的整式
的整式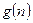 ,使得
,使得 对于一切不小于2的自然数
对于一切不小于2的自然数 恒成立? 若存在,写出
恒成立? 若存在,写出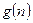 的解析式,并加以证明;若不存在,试说明理由。
的解析式,并加以证明;若不存在,试说明理由。
设斜率为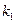 的直线
的直线 交椭圆
交椭圆 :
: 于
于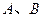 两点,点
两点,点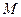 为弦
为弦 的中点,直线
的中点,直线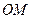 的斜率为
的斜率为 (其中
(其中 为坐标原点,假设
为坐标原点,假设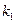 、
、 都存在).
都存在).
(1)求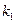 ×
× 的值.
的值.
(2)把上述椭圆 一般化为
一般化为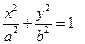 (
(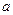 >
>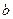 >0),其它条件不变,试猜想
>0),其它条件不变,试猜想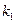 与
与 关系(不需要证明).请你给出在双曲线
关系(不需要证明).请你给出在双曲线 (
(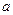 >0,
>0,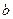 >0)中相类似的结论,并证明你的结论.
>0)中相类似的结论,并证明你的结论.