等比数列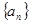 中,
中,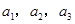 分别是下表第一
分别是下表第一 、二、三行中的某一个数,且
、二、三行中的某一个数,且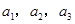 中的任何两个数不在下表的同一列
中的任何两个数不在下表的同一列
| |
第一列 |
第二列 |
第三列 |
| 第一行 |
3 |
2 |
10 |
| 第二行 |
6 |
4 |
14 |
| 第三行 |
9 |
8 |
18 |
(Ⅰ)求数列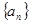 的通项公式。
的通项公式。
(Ⅱ)若数列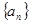 满足:
满足: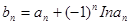 ,求数列
,求数列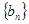 的
的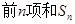 。
。
已知函数 ,(
,( )在
)在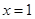 处取得最小值.
处取得最小值.
(Ⅰ)求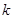 的值;
的值;
(Ⅱ)若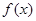 在
在 处的切线方程为
处的切线方程为 ,求证:当
,求证:当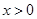 时,曲线
时,曲线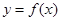 不可能在直线
不可能在直线 的下方;
的下方;
(Ⅲ)若 ,(
,( )且
)且 ,试比较
,试比较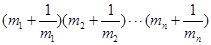 与
与 的大小,并证明你的结论.
的大小,并证明你的结论.
已知函数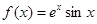 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的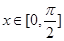 ,
,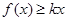 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
(Ⅲ)设函数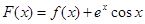 ,
,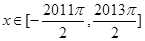 ,过点
,过点 作函数
作函数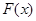 图象的所有切线,令各切点得横坐标构成数列
图象的所有切线,令各切点得横坐标构成数列 ,求数列
,求数列 的所有项之和
的所有项之和 的值.
的值.
湖北宜昌“三峡人家”风景区为提高经济效益,现对某一景点进行改造升级,从而扩大内需,提高旅游增加值,经过市场调查,旅游增加值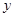 万元与投入
万元与投入 万元之间满足:
万元之间满足: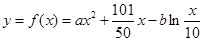 ,
, 为常数,当
为常数,当 万元时,
万元时, 万元;当
万元;当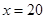 万元时,
万元时, 万元.(参考数据:
万元.(参考数据: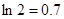 ,
,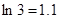 ,
,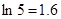 )
)
(Ⅰ)求 的解析式;
的解析式;
(Ⅱ)求该景点改造升级后旅游利润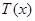 的最大值.(利润=旅游收入-投入)
的最大值.(利润=旅游收入-投入)
已知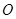 为坐标原点,向量
为坐标原点,向量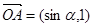 ,
,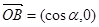 ,
,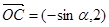 ,点
,点 满足
满足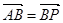 .
.
(Ⅰ)记函数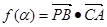 ,
,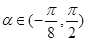 ,讨论函数
,讨论函数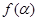 的单调性,并求其值域;
的单调性,并求其值域;
(Ⅱ)若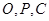 三点共线,求
三点共线,求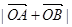 的值.
的值.
已知命题 ,
, ,命题
,命题 ,使得
,使得 .若“
.若“ 或
或 为真”,“
为真”,“ 且
且 为假”,求实数
为假”,求实数 的取值范围.
的取值范围.