已知函数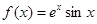 .
.
(Ⅰ)求函数 的单调区间;
的单调区间;
(Ⅱ)如果对于任意的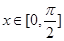 ,
,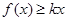 总成立,求实数
总成立,求实数 的取值范围;
的取值范围;
(Ⅲ)设函数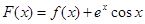 ,
,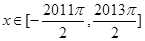 ,过点
,过点 作函数
作函数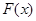 图象的所有切线,令各切点得横坐标构成数列
图象的所有切线,令各切点得横坐标构成数列 ,求数列
,求数列 的所有项之和
的所有项之和 的值.
的值.
选修4-4:坐标系与参数方程
已知曲线C的极坐标方程是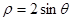 ,直线
,直线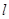 的参数方程是
的参数方程是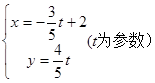 。
。
(1)将曲线C的极坐标方程化为直角坐标方程;
(2)设直线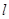 与
与 轴的交点是M,N是曲线C上一动点,求
轴的交点是M,N是曲线C上一动点,求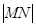 的最大值。
的最大值。
选修4-1:几何证明选讲
如图,圆O的半径OB垂直于直径AC,M为OA上一点,BM的延长线交圆O于N,过N点的切线交CA的延长线于P。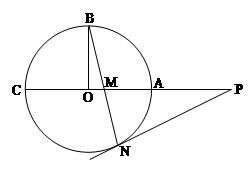
(1)求证:PM2=PA·PC
(2)若圆O的半径为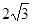 ,OA=
,OA= OM,求MN的长。
OM,求MN的长。
已知函数 。
。
(1)若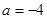 ,求函数
,求函数 的单调区间;
的单调区间;
(2)若函数 在
在 上单调递增,求实数
上单调递增,求实数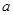 的取值范围;
的取值范围;
(3)记函数 ,若
,若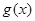 的最小值是
的最小值是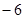 ,求函数
,求函数 的解析式。
的解析式。
已知椭圆方程为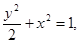 斜率为
斜率为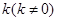 的直线过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴交于点M(0,m)。
的直线过椭圆的上焦点且与椭圆相交于P,Q两点,线段PQ的垂直平分线与y轴交于点M(0,m)。
(1)求m的取值范围;
(2)求△OPQ面积的取值范围。
如图,四棱锥P-ABCD中底面ABCD为矩形,PD⊥底面ABCD,AD=PD=1,AB=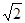 BC,E、F分别为CD、PB的中点。
BC,E、F分别为CD、PB的中点。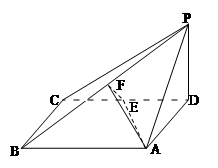
(1)求证:EF⊥平面PAB;
(2)求三棱锥P-AEF的体积