一座拱型桥,桥下水面宽度AB是20米,拱高CD是4米.若水面上升3米至EF,则水面宽度EF是多少?若把它看作是抛物线的一部分,在坐标系中(如图1)可设抛物线的表达式为
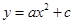 .
.
请你填空:a= ,c= ,EF= 米.若把它看作是圆的一部分,则可构造图形(如图2)计算如下:
设圆的半径是r米,在Rt△OCB中,易知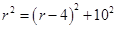 ,r=14.5
,r=14.5
同理,当水面上升3米至EF,在Rt△OGF中可计算出GF= 米,即水面宽度EF= 米.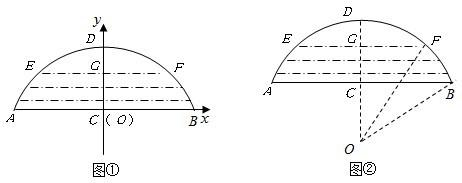
有一块三角形的地,现要平均分给四农户种植(即四等分三角形面积)请你在图上作出分法.(不写作法,保留作图痕迹)
附加题:等边三角形给人以“稳如泰山”的美感,它具有独特的对称性,请你用两种不同的分割方法,将以下两个等边三角形分别割成四个等腰三角形.(在图中画出分割线,并标出必要的角的度数)
如图,△ABC≌△DEF,求证:AD=BE.
△ABC≌△DEF,且△ABC的周长为18.若AB等于5,EF等于6,求AC的值.
如图,△ABC中,∠ACB=90°,AC=6,BC=8.点P从A点出发沿A﹣C﹣B路径向终点运动,终点为B点;点Q从B点出发沿B﹣C﹣A路径向终点运动,终点为A点.点P和Q分别以1和3的运动速度同时开始运动,两点都要到相应的终点时才能停止运动,在某时刻,分别过P和Q作PE⊥l于E,QF⊥l于F.问:点P运动多少时间时,△PEC与QFC全等?请说明理由.