12分)某工厂对200个电子元件的使用寿命进行检查,按照使用寿命(单位:h),可以把这批电子元件分成第一组[100,200],第二组(200,300],第三组(300,400],第四组(400,500],第五组(500,600],第六组(600,700].由于工作中不慎将部分数据丢失,现有以下部分图表: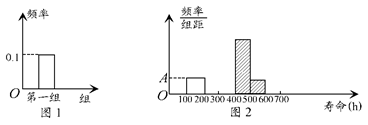
| 分组 |
[100,200] |
(200,300] |
(300,400] |
(400,500] |
(500,600] |
(600,700] |
| 频数 |
B |
30 |
E |
F |
20 |
H |
| 频率 |
C |
D |
0.2 |
0.4 |
G |
I |
(1)求图2中的A及表格中的B,C,D,E,F,G,H,I的值;
(2)求图2中阴影部分的面积;
(3)若电子元件的使用时间超过300h为合格产品,求这批电子元件合格的概率.
(本小题满分15分)
已知: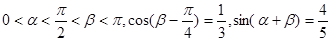 .
.
(1)求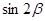 的值;
的值;
(2)求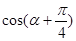 的值.
的值.
(本小题满分14分)
某化工企业2011年底投入100万元,购入一套污水处理设备.该设备每年的运转费用是0.5万元,此外每年都要花费一定的维护费,第一年的维护费为2万元,由于设备老化,以后每年的维护费都比上一年增加2万元.
(1)求该企业使用该设备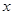 年的年平均污水处理费用
年的年平均污水处理费用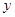 (万元);(污水处理费包括设备购买费用、运转费和维护费)
(万元);(污水处理费包括设备购买费用、运转费和维护费)
(2)问为使该企业的年平均污水处理费用最低,该企业几年后需要重新更换新的污水处理设备?
(本小题满分14分)
已知集合 ,
,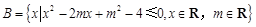 .
.
(1)若 ,求实数
,求实数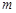 的值;
的值;
(2)若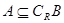 ,求实数
,求实数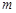 的取值范围.
的取值范围.
某班级共派出 个男生和
个男生和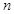 个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有
个女生参加学校运动会的入场仪式,其中男生甲为领队.入场时,领队男生甲必须排第一个,然后女生整体在男生的前面,排成一路纵队入场,共有 种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有
种排法;入场后,又需从男生(含男生甲)和女生中各选一名代表到主席台服务,共有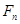 种选法.
种选法.
(1)试求 和
和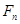 ;
;
(2)判断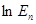 和
和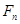 的大小(
的大小(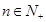 ),并用数学归纳法证明.
),并用数学归纳法证明.
某学校设计了一个实验学科的考查方案:考生从6道备选题中一次性抽取3道题,规定至少正确完成其中2道题便可通过,已知6道备选题中考生甲有4道能正确完成,2道不能完成;考生乙正确完成每道题的概率都是 ,且每题正确完成与否互不影响.
,且每题正确完成与否互不影响.
⑴求甲正确完成的题数 的分布列及期望;求乙正确完成的题数
的分布列及期望;求乙正确完成的题数 的分布列及期望;
的分布列及期望;
⑵请用统计知识分析比较两名考生这门学科的水平.