从参加环保知识竞赛的学生中抽出60名，将其成绩（均为整数）整理后画出的频率分布直方图如下：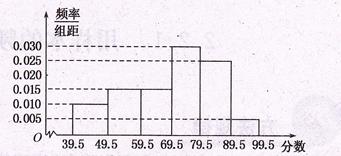
观察图形，回答下列问题：
（1）79.5～89.5这一组的频数、频率分别是多少？
（2）估计这次环保知识竞赛的及格率（60分以上为及格）。
（本小题满分10分）【选修4-4：坐标系与参数方程】
在平面直角坐标系xOy中，已知曲线C：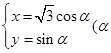
为参数），以平面直角坐标系xOy的原点O为极点，x轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线l：
=6．
（1）在曲线C上求一点P，使点P到直线l的距离最大，并求出此最大值；
（2）过点M（一1，0）且与直线l平行的直线l1交C于A, B两点，求点M到A，B两点的距离之积．
（本小题满分10分）【选修4一1：几何证明选讲】
如图，已知圆的两条弦AB, CD，延长AB，CD交于圆外一点E，过E作AD的平行线交CB的延长线于F，过点F作圆的切线FG，G为切点．求证：
（1）△EFC∽△BFE；
（2）FG＝FE
（本小题满分12分）已知f（x）＝
。
（1）曲线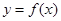
在点（1，f（1））处的切线斜率为0，求f（x）的单调区间；
（2）若f（x）＜x2在（1，＋
）恒成立，求a的取值范围。
（本小题满分12分）已知椭圆C：
的离心率为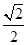
，连接椭圆四个顶点形成的四边形面积为4
．
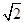（1）求椭圆C的标准方程；
（2）过点A（1，0）的直线与椭圆C交于点M, N,设P为椭圆上一点，且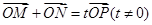
O为坐标原点，当
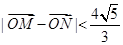时，求t的取值范围．
（本小题满分12分）如图，在三棱锥S -ABC中，△ABC是边长为2的正三角形，平面SAC⊥平面ABC，SA=SC＝
，M为AB的中点．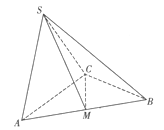
（1）证明：AC⊥SB；
（2）求点B到平面SCM的距离。