(本小题满分12分)设函数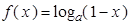 ,
, (
(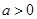 且
且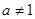 )。
)。
(1)设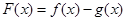 ,判断
,判断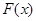 的奇偶性并证明;
的奇偶性并证明;
(2)若关于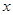 的方程
的方程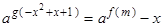 有两个不等实根,求实数
有两个不等实根,求实数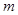 的范围;
的范围;
某工厂生产甲、乙两种产品,已知生产每吨甲、乙两种产品所需煤、电力、劳动力、获得利润及每天资源限额(最大供应量)如下表所示:
 产品 产品消耗量 资源 |
甲产品(每吨) |
乙产品(每吨) |
资源限额(每天) |
| 煤(t) |
9 |
4 |
360 |
| 电力(kw·h) |
4 |
5 |
200 |
| 劳动力(个) |
3 |
10 |
300 |
| 利润(万元) |
6 |
12 |
问:每天生产甲、乙两种产品各多少吨,获得利润总额最大?
如图所示,在棱长为2的正方体 中,
中, 、
、 分别为
分别为 、
、 的中点.
的中点.
(Ⅰ)求证: //平面
//平面 ;
;
(Ⅱ)求证: ;
;
由于当前学生课业负担较重,造成青少年视力普遍下降,现从某中学随机抽取16名学生,经校医用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下:
(1)指出这组数据的众数和中位数;
(2)若视力测试结果不低于5.0,则称为“good sight”,若校医从“good sight”,中随机选取2人,试求抽到视力有5.2的学生的概率。
已知函数 .
.
(Ⅰ)若点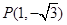 在角
在角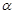 的终边上,求
的终边上,求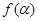 的值;
的值;
(Ⅱ)若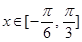 ,求
,求 的值域.
的值域.
(14分)已知定义在R上的函数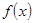 对任意
对任意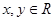 都有
都有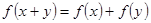 ,且当
,且当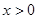 时,
时,
(1)求证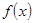 为奇函数;
为奇函数;
(2)判断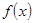 在R上的单调性,并用定义证明;
在R上的单调性,并用定义证明;
(3)若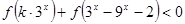 ,对任意
,对任意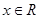 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。