对于三次函数
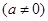 .
.
定义:(1)设 是函数
是函数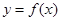 的导数
的导数 的导数,若方程
的导数,若方程 有实数解
有实数解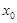 ,则称点
,则称点 为函数
为函数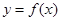 的“拐点”;
的“拐点”;
定义:(2)设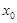 为常数,若定义在
为常数,若定义在 上的函数
上的函数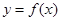 对于定义域内的一切实数
对于定义域内的一切实数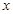 ,都有
,都有 成立,则函数
成立,则函数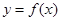 的图象关于点
的图象关于点 对称.
对称.
己知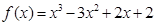 ,请回答下列问题:
,请回答下列问题:
(1)求函数 的“拐点”
的“拐点” 的坐标
的坐标
(2) 检验函数
检验函数 的图象是否关于“拐点”
的图象是否关于“拐点” 对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
对称,对于任意的三次函数写出一个有关“拐点”的结论(不必证明)
(3)写出一个三次函数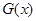 ,使得它的“拐点”是
,使得它的“拐点”是 (不要过程)
(不要过程)
直线
与椭圆
相交于
两点,
为坐标原点.
(Ⅰ)当点
的坐标为
,且四边形
为菱形时,求
的长;
(Ⅱ)当点
在
上且不是
的顶点时,证明:四边形
不可能为菱形.
已知函数
.
(Ⅰ)若曲线
在点
处与直线
相切,求
与
的值.
(Ⅱ)若曲线
与直线
有两个不同的交点,求
的取值范围.
如图,在四棱锥
中,
,平面
底面
,
.
和
分别是
和
的中点,求证: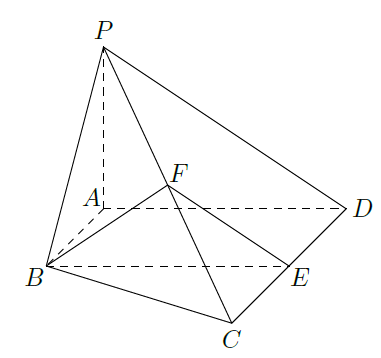
(Ⅰ)
底面
;
(Ⅱ)
平面
;
(Ⅲ)平面
平面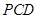
下图是某市3月1日至14日的空气质量指数趋势图,空气质量指数小于100表示空气质量优良,空气质量指数大于200表示空气重度污染,某人随机选择3月1日至3月15日中的某一天到达该市,并停留2天.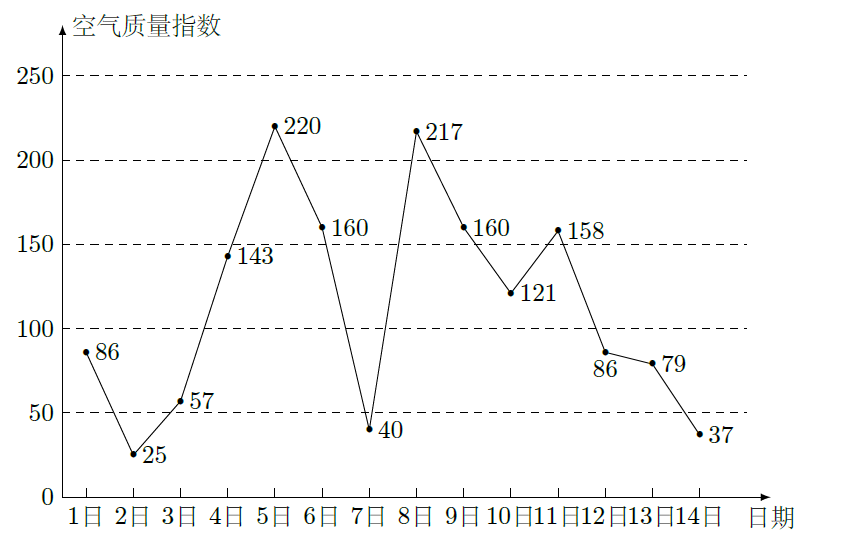
(Ⅰ)求此人到达当日空气质量优良的概率;
(Ⅱ)求此人在该市停留期间只有1天空气重度污染的概率;
(Ⅲ)由图判断从哪天开始连续三天的空气质量指数方差最大?(结论不要求证明)
已知函数
(Ⅰ)求
的最小正周期及最大值;
(Ⅱ)若
,且
,求
的值.