已知函数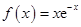
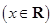 .
.
(1)求函数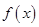 的单调区间和极值;
的单调区间和极值;
(2)已知函数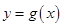 的图象与函数
的图象与函数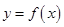 的图象关于直线
的图象关于直线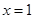 对称.证明当
对称.证明当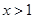 时,
时,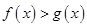 ;
;
(3)如果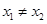 ,且
,且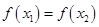 ,证
,证 明
明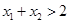
如图,已知抛物线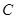 :
: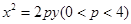 ,其上一点
,其上一点 到其焦点
到其焦点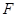 的距离为
的距离为 ,过焦点
,过焦点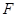 的直线
的直线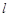 与抛物线
与抛物线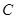 交于
交于 左、右两点.
左、右两点.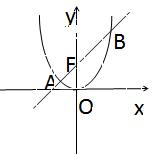
(1)求抛物线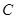 的标准方程;
的标准方程;
(2)若 ,求直线
,求直线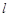 的方程.
的方程.
已知椭圆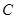 :
: 的离心率为
的离心率为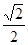 ,
, 是椭圆
是椭圆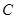 的左焦点.
的左焦点.
(1)求椭圆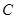 的方程;
的方程;
(2)若直线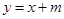 与椭圆
与椭圆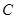 相交于不同的两点
相交于不同的两点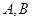 .且线段
.且线段 的中点
的中点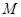 在圆
在圆 上,求
上,求 的值.
的值.
已知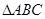 的三个顶点的坐标为
的三个顶点的坐标为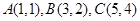 .
.
(1)求 边上的高所在直线的方程;
边上的高所在直线的方程;
(2)若直线 与
与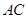 平行,且在
平行,且在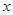 轴上的截距比在
轴上的截距比在 轴上的截距大1,求直线
轴上的截距大1,求直线 与两条坐标轴围成的三角形的周长.
与两条坐标轴围成的三角形的周长.
已知函数 ,若函数
,若函数 的最小值是
的最小值是 且对称轴是
且对称轴是 ,
, .
.
(1)求 的值;
的值;
(2)在(1)条件下求 在区间
在区间
 的最小值.
的最小值.
已知函数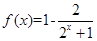 .
.
(1)证明 是奇函数;
是奇函数;
(2)判断 的单调性,并用定义证明;
的单调性,并用定义证明;
(3)求 在[-1,2] 上的最值.
在[-1,2] 上的最值.