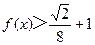已知平面向量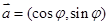 ,
,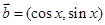 ,
,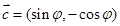 ,其中
,其中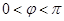 ,且函数
,且函数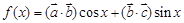 的图象过点
的图象过点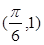 .(Ⅰ)求
.(Ⅰ)求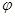 的值;
的值;
(Ⅱ)将函数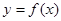 图象上各点的横坐标伸长为原来的的2倍,纵坐标不变,得到函数
图象上各点的横坐标伸长为原来的的2倍,纵坐标不变,得到函数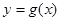 的图象,求函数
的图象,求函数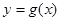 在
在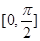 上的最大值和最小值
上的最大值和最小值
某项选拔共有三轮考核,每轮设有一个问题,能正确回答问题者进入下一轮考试,否则即被淘汰,已知某选手能正确回答第一、二、三轮的问题的概率分别为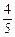 、
、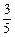 、
、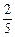 ,且各轮问题能否正确回答互不影响.
,且各轮问题能否正确回答互不影响.
(Ⅰ)求该选手被淘汰的概率;
(Ⅱ)该选手在选拔中回答问题的个数记为ξ,求随机变量ξ的分布列与数数期望.(注:本小题结果可用分数表示)
已知甲盒内有大小相同的3个红球和4个黑球,乙盒内有大小相同的5个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为红球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球.现从甲、乙两个盒内各任取2个球.
(Ⅰ)求取出的4个球均为黑球的概率;
(Ⅱ)求取出的4个球中恰有1个红球的概率;
(Ⅲ)设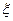 为取出的4个球中红球的个数,求
为取出的4个球中红球的个数,求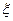 的分布列和数学期望.
的分布列和数学期望.
厂家在产品出厂前,需对产品做检验,厂家将一批产品发给商家时,商家按合同规定也需随机抽取一定数量的产品做检验,以决定是否接收这批产品.
(Ⅰ)若厂家库房中的每件产品合格的概率为0.8,从中任意取出4件进行检验.求至少有1件是合格品的概率;
(Ⅱ)若厂家发给商家20件产品,其中有3件不合格,按合同规定该商家从中任取2件,都进行检验,只有2件都合格时才接收这批产品,否则拒收.求该商家可能检验出不合格产品数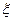 的分布列及期望
的分布列及期望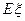 ,并求该商家拒收这批产品的概率.
,并求该商家拒收这批产品的概率.
已知函数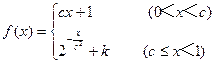 在区间(0,1)内连续,且
在区间(0,1)内连续,且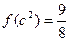 .
.
(1)求实数k和c的值;
(2)解不等式