近年来,全球气候变化无常,给人们的生产与生活该来诸多不便.为研究气候的变化趋势,给我们的生产与生活提供有力的数据支持,某市气象部门统计了共100个星期中每个星期气温的最高温度和最低温度,如表所示:
(Ⅰ)若第六、七、八组的频数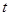 、
、 、
、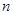 为递减的等差数列,且第一组与第八组的频数相同,求出
为递减的等差数列,且第一组与第八组的频数相同,求出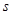 、
、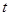 、
、 、
、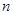 的值;
的值;
(Ⅱ)若从第一组和第八组的所有星期中随机抽取两个星期,分别记它们的平均温度为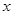 ,
,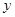 ,求事件“
,求事件“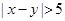 ”的概率.
”的概率.
已知幂函数 上是增函数,
上是增函数, ,
,
(1)当 时,求
时,求 的值;
的值;
(2)求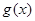 的最值以及
的最值以及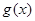 取最值时x的取值集合.
取最值时x的取值集合.
在 中,角
中,角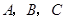 的对边分别为
的对边分别为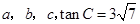 .
.
(1)求 ;
;
(2)若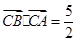 ,且
,且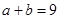 ,求
,求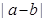 .
.
已知函数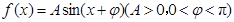 ,
,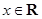 的最大值是1,其图像经过点
的最大值是1,其图像经过点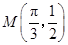 .
.
(1)求 的解析式;
的解析式;
(2)已知 ,且
,且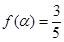 ,
,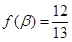 ,求
,求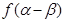 的值.
的值.
已知函数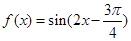 ,
,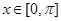
(Ⅰ)用“五点法”在所给的直角坐标系中画出函数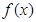 的图像.
的图像.
(Ⅱ)写出 的图象是由
的图象是由 的图象经过怎样的变换得到的.
的图象经过怎样的变换得到的.
下面是一周内某地申领结婚证的新郎与新娘的年龄,记作(新郎年龄y,新娘年龄x):
(37,30),(30,27),(65,56),(45,40),(32,30),(28,26),(45,31),(29,24),(26,23),(28,25),(42,29),(36,33),(32,29),(24,22),(32,33),(ZI,29),(37,46),(28,25),(33,34),(21,23),(24,23),(49,44),(28,29),(30,30),(24,25),(22,23),(68,60),(25,25),(32,27),(42,37),(24,24),(24,22),(28,27),(36,31),(23,24),(30,26)
以下考虑y关于x的回归问题:
(1)如果每个新郎和新娘都同岁,穿过这些点的回归直线的斜率和截距等于什么?
(2)如果每个新郎比他的新娘大5岁,穿过这些点的回归直线的斜率和截距等于什么?
(3)如果每个新郎比他的新娘大10%,穿过这些点的回归直线的斜率和截距等于什么?
(4)对于上面的实际年龄作出回归直线;
(5)从这条回归直线,你对新娘和新郎的年龄模型可得出什么结论?