如图,在四棱锥S-ABCD中,AB⊥AD,AB∥CD,CD=3AB=3,平面SAD⊥平面ABCD,E是线段AD上一点,AE=ED= ,SE⊥AD.
,SE⊥AD.
(Ⅰ)证明:平面SBE⊥平面SEC;
(Ⅱ)若SE=1,求直线CE与平面SBC所成角的正弦值.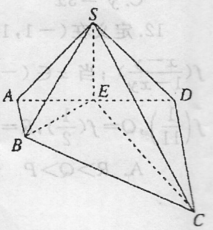
已知函数 。
。
(Ⅰ)确定 在
在 上的单调性;
上的单调性;
(Ⅱ)设 在
在 上有极值,求
上有极值,求 的取值范围。
的取值范围。
已知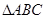 的三个内角A、B、C所对的边分别为
的三个内角A、B、C所对的边分别为 ,向量
,向量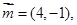
 ,且
,且 .
.
(1)求角A的大小;
(2)若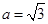 ,试判断
,试判断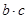 取得最大值时
取得最大值时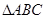 形状.
形状.
已知集合A= ,B=
,B= ,
,
(1)当 时,求
时,求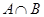
(2)若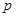 :
: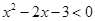 ,
, :
: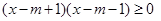 ,且
,且 是
是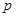 的必要不充分条件,求实数
的必要不充分条件,求实数 的取值范围。
的取值范围。
(本小题满分12分)已知直线L:y=x+1与曲线C: 交于不同的两点A,B;O为坐标原点。
交于不同的两点A,B;O为坐标原点。
(1)若 ,试探究在曲线C上仅存在几个点到直线L的距离恰为
,试探究在曲线C上仅存在几个点到直线L的距离恰为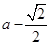 ?并说明理由;
?并说明理由;
(2)若 ,且a>b,
,且a>b, ,试求曲线C的离心率e的取值范围。
,试求曲线C的离心率e的取值范围。
(本小题满分12分) 甲乙共同拥有一块形状为等腰三角形的地ABC,其中 。如果画一条线使两块地面积相等,其中两端点P、Q分别在线段AB,AC上。
。如果画一条线使两块地面积相等,其中两端点P、Q分别在线段AB,AC上。
(1)如果建一条篱笆墙,如何划线建墙费用最低?
(2)如果在PQ线上种树,如何划线种树最多?