(本小题满分14分)设椭圆方程 (
( ),
), 为椭圆右焦点,
为椭圆右焦点, 为椭圆在短轴上的一个顶点,
为椭圆在短轴上的一个顶点, 的面积为6,(
的面积为6,( 为坐标原点);
为坐标原点);
(1)求椭圆方程;
(2)在椭圆上是否存在一点 ,使
,使 的中垂线过点
的中垂线过点 ?若存在,求出
?若存在,求出 点坐标;若不存在,说明理由.
点坐标;若不存在,说明理由.
某企业2010年的纯利润为500万元,因设备老化等原因,企业的生产能力将逐年下降。若不能进行技术改造,预测从今年起每年比上一年纯利润减少20万元,今年初该企业一次性投入资金600万元进行技术改造,预测在 末扣除技术资金的情况下,第n年(2011年为第一年)的利润为500(1+
末扣除技术资金的情况下,第n年(2011年为第一年)的利润为500(1+ )万元(n为正整数)
)万元(n为正整数)
(1)设从今年起的前n年,若该企业不进行技术改造的累计纯利润为 万元,进行技术改造后的累计纯利润为
万元,进行技术改造后的累计纯利润为 万元(须扣除技术改造资金),求
万元(须扣除技术改造资金),求 、
、 的表达式;
的表达式;
(2)依上述预测,从今年起该企业至少经过多少年,进行技术改造后的累计纯利润超过不进行技术改造的累计纯利润?
、已知点M在椭圆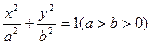 上,以M为圆心的圆与x轴相切于椭圆的右焦点F。
上,以M为圆心的圆与x轴相切于椭圆的右焦点F。
(1)若圆M与y轴相切,求椭圆的离心 率;
率;
(2)若圆M与y轴相交于A、B两点,且△ABM是边长为2的正三角形,求椭圆的方程。
如图,已知四棱锥P—ABCD中,底面ABCD的直角梯形,AB//DC,
∠ABC=45°,DC=1,AB=2,PA⊥平面ABCD,PA=1。
(1)求证:AB//平 面PCD;
面PCD;
(2)求证:BC⊥平面PAC;
(3)若M是PC的中点,求三棱锥M—ACD的体积。
、已知向量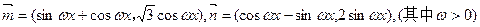 ,
,
函数 ,若
,若 相邻两对称轴间的距离为
相邻两对称轴间的距离为 。
。
(1)求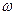 的值
的值 ,并求
,并求 的最大值及相应x的集合;
的最大值及相应x的集合;
(2)在△ABC中,a,b,c分别是A,B,C所对的边,△AB C的面积
C的面积 ,求边a的长。
,求边a的长。
为检测学生的体温状况,随机抽取甲,乙两个班各10名同学,测量他们的体温(单位0.1摄氏度)获得体温数据的茎叶图,如图所示。
(1)计算乙班的样本平均数,方差;
(2)现在从甲班中随机抽取两名体温不低于36.5摄氏
度的同学,求体温为37.1摄氏度的同学被抽到的概率