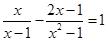小明用下面的方法求出方程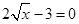 的解,请你仿照他的方法求出下
的解,请你仿照他的方法求出下
面另外两个方程的解,并把你的解答过程填写在下面的表格中.
| 方程 |
换元法得新方程 |
解新方程 |
检验 |
求原方程的解 |
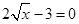 |
令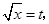 则 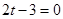 |
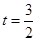 |
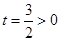 |
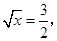 所以 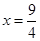 |
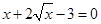 |
|
|
|
|
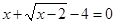 |
|
|
|
|
在平行四边形ABCD中,E为BC边上的一点.连结AE.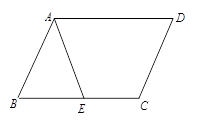
(1)若AB=AE, 求证:∠DAE=∠D;
(2)若点E为BC的中点,连接BD,交AE于F,求EF︰FA的值.
在平面直角坐标系中,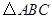 的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
的三个顶点坐标分别为A(2,-4),B(3,-2), C(6,-3).
(1)画出△ABC关于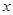 轴对称的△A1B1C1;
轴对称的△A1B1C1;
(2)以M点为位似中心,在网格中画出△A1B1C1的位似图形△A2B2C2 ,使△A2B2C2与△A1B1C1的相似比为2︰1.
为了解中考体育科目训练情况,某地从九年级学生中随机抽取了部分学生进行了一次考前体育科目测试,把测试结果分为四个等级: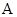 级:优秀;
级:优秀;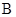 级:良好;
级:良好; 级:及格;
级:及格; 级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题:
级:不及格,并将测试结果绘成了如下两幅不完整的统计图.请根据统计图中的信息解答下列问题: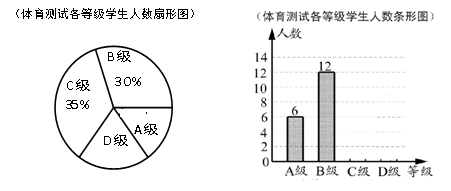
(1)请将两幅不完整的统计图补充完整;
(2)如果该地参加中考的学生将有4500名,根据测试情况请你估计不及格的人数有多少?
(3)从被抽测的学生中任选一名学生,则这名学生成绩是 级的概率是多少?
级的概率是多少?
解不等式组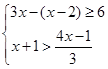
解方程: