(本小题满分8分)(神奇的数学游戏)根据下面的游戏向导来试着玩这个游戏。
写出一个你喜欢的数,把这个数加上2,把结果乘以5,再减去10,再除以5,结果你会重新得到原来的数。(1)假设一开始写出的数为n,根据这个游戏的每一步,列出最后的表达式。
(2)将(1)中得到的表达式进行化简。请你说明:为什么游戏对任意数都成立。
以下统计图描述了九年级(1)班学生在为期一个月的读书月活动中,三个阶段(上旬、中旬、 下旬)日人均阅读时间的情况:
(1)从统计图可知,九年级(1)班共有学生多少人?
(2)求图22.1中a的值
(3)从图22-1、22-2 中判断,在这次读书月活动中,该班学生每日阅读时间_______(填“普遍增加了”或“普遍减少了”):
(4)通过这次读书月活动,如果该班学生初步形成了良好的每日阅读习惯,参照以上统计图的变化趋势,至读书月活动结束时,该班学生日人均阅读时间在0.5~1(即0.5≤t<10)小 时的人数比活动开展初期增加了多少人?
频数(学生人数)活动上旬频数分布直方图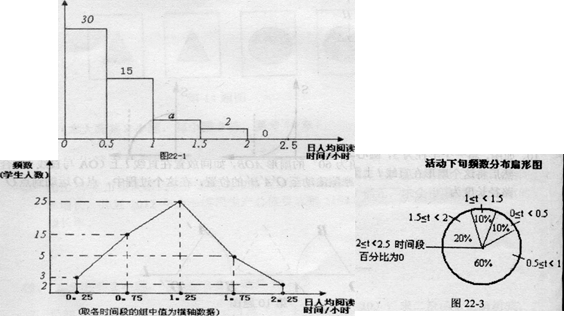
(每个小矩形含左端点,不含右端点)
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E, 连接DE,F为线段DE上一点,且∠AFE=∠B.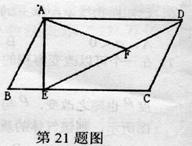
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3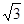 ,AE=3,求AF的长.
,AE=3,求AF的长.
在东西方向的海岸线,上有一长为1km的码头MN(如图,MN=lkm),在码头西端M的正西19.5 km处有一观察站A.某时刻测得一艘匀速直线航行的轮船位于A的北偏西3000,且与A相距40km的B处;经过l小时20分钟,又测得该轮船位于A的北偏东6000方向,且与A相距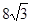 km的C处.
km的C处.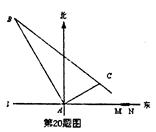
(1)求该轮船航行的速度(保留精确结果);
(2)如果该轮船不改变航向继续航行,那么轮船能否正好行至码头MN靠岸?请说明理由.
如图,若反比例函数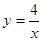 与一次函数y=mx-1的图象都经过点A(-4,a)
与一次函数y=mx-1的图象都经过点A(-4,a)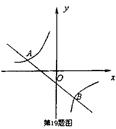
(1)求a和m的值。
(2)在第二象限内,利用函数图象直接写出,mx-1>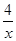 的解集.
的解集.
命题:若三角形的三边的长度均大于4,则它的面积一定大于l.
在下面的平面直角坐标系中画出图形,并利用该图形说明该命题为假命题(即指出你所画图形 的边均大于4,而面积不大于1)。